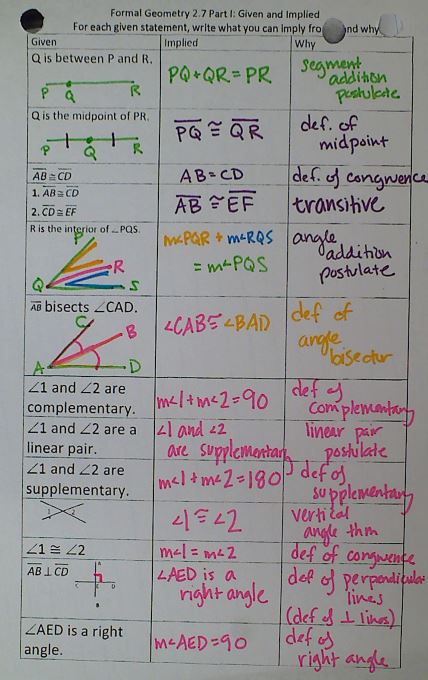
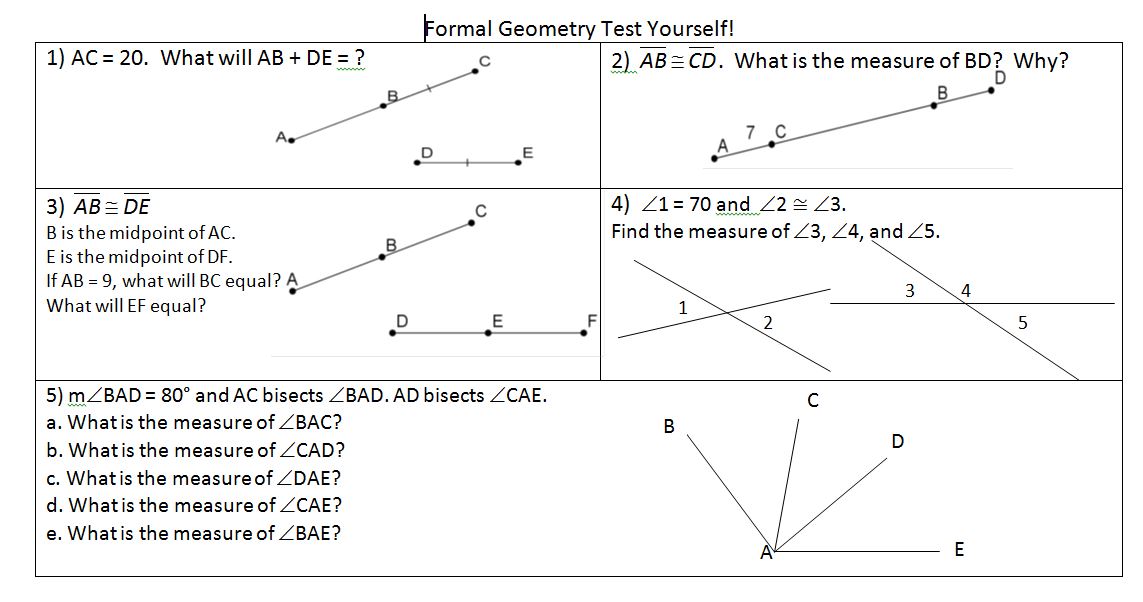
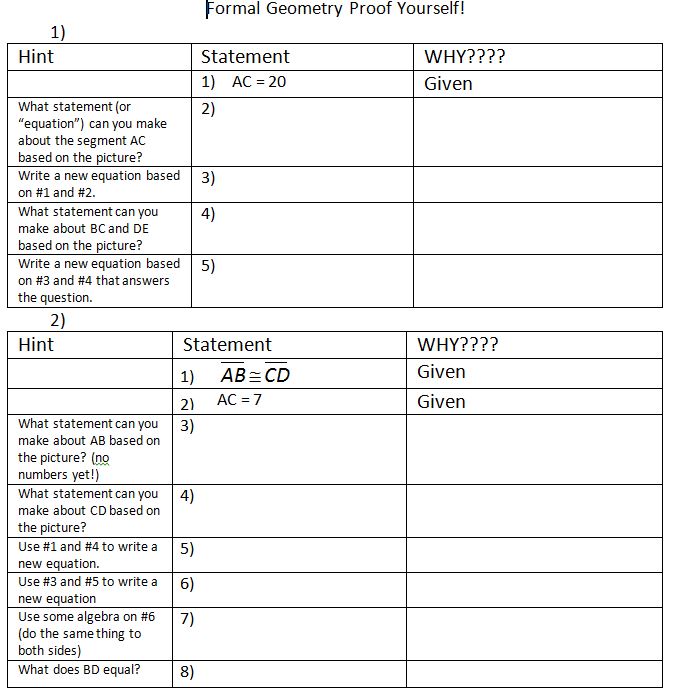
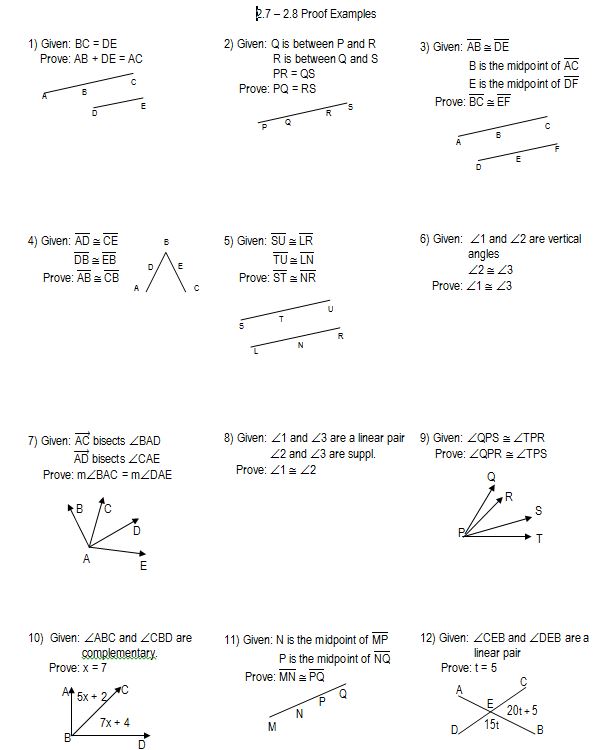
tl;dr: notes, homework, and study guides for solving systems, graphing systems, and linear programming
Ok, I’m in the mood to knock some more of these posts out. See more Algebra II files and FAQs here.
As teachers, we divvied up some chapters a couple years ago to try and fancy them up, so some of this was found by my co-teacher and not made by me. We were really pressed for time this year, so I had to cut out this intro activity that I had success with in the past (and, yes, it’s for Algebra I…don’t tell!):
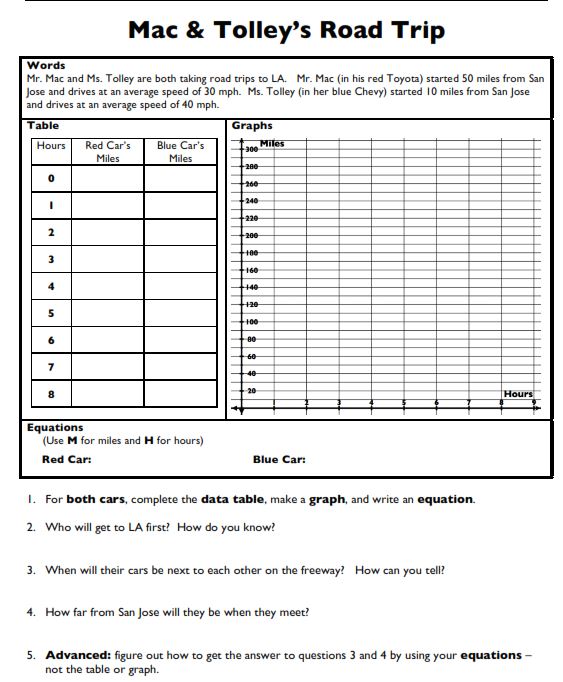Download it here. I really liked this part:
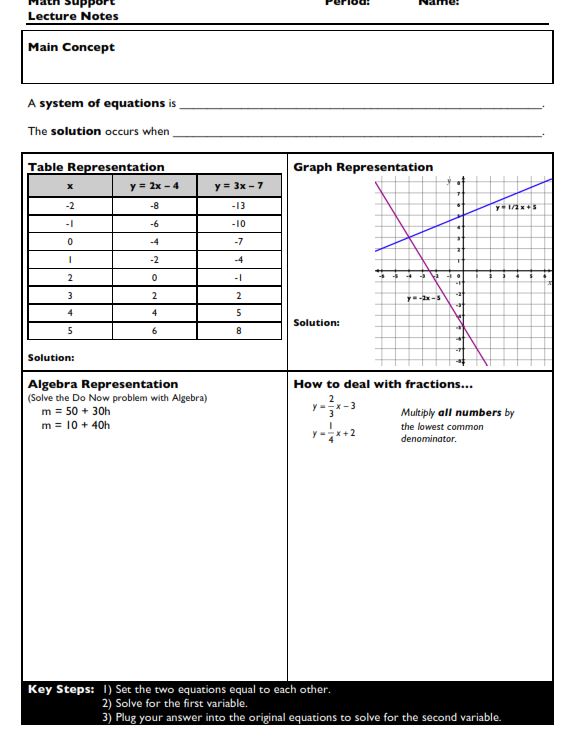I like this idea of an introductory activity as well:
But I can’t find the source so I don’t have the worksheet with points (although I guess I could make my own.) Anyone recognize it?!?!? Please??!!?
We then do some formal solve with graphing:
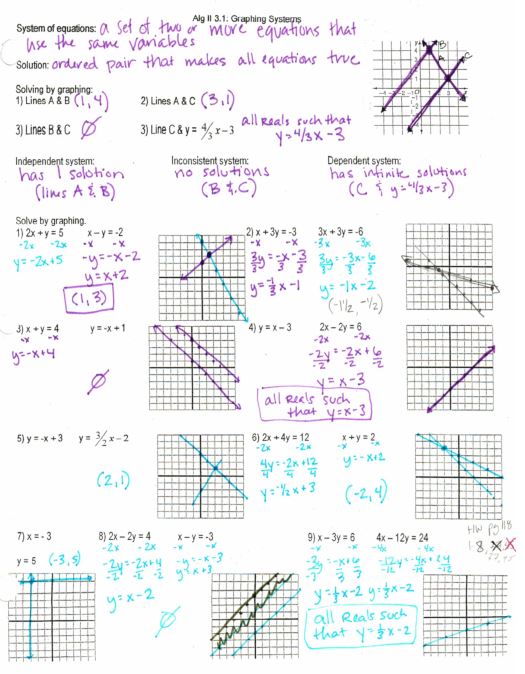Ok, this is awkward…this file is so old, I don’t have a blank version on my computer! But you get the idea. 🙂
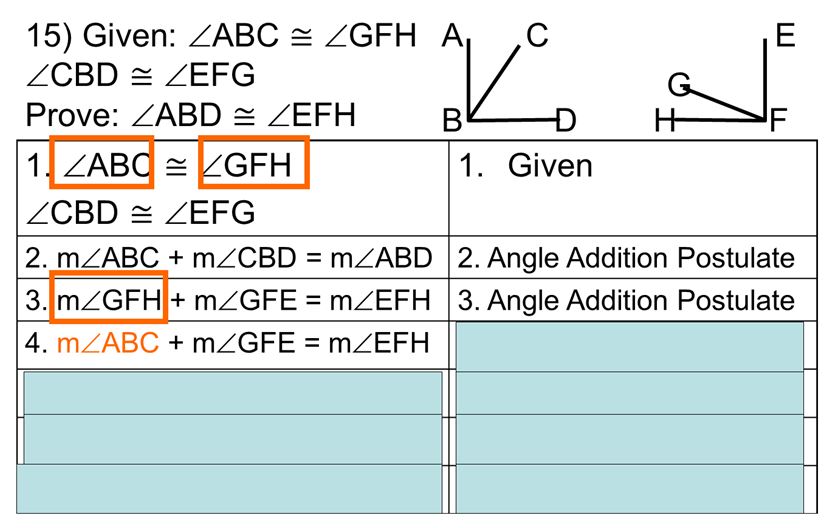
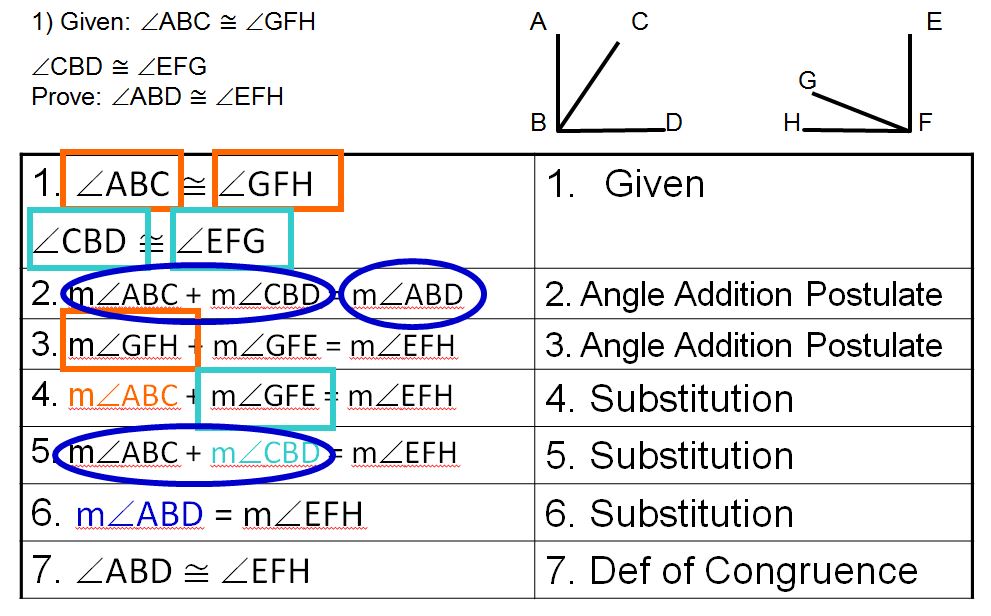
No notetakermaker for solving systems by substitution or elimination (we take them on our own paper or else it gets a wee bit scrunched). But here’s a tip: talk about substituting is just like substituting a player on a team because (1) some players are more beneficial are certain times in the game (ooh, I just thought of this…do the players have to also be “equivalent”? As in, I assume you substitute a defensive player for another defensive player?) and (2) you can’t have both players on the field. That seemed to help so struggling students not substitute y = 7x + 2 into 3y + 9x = 8 as “3y(7x + 2) + 9x = 8.” Also, it makes me seem like I know about sports. (Obviously false.)
Some homework:
File here. And in case you need some word problems:
File here. And some linear inequalities systems:
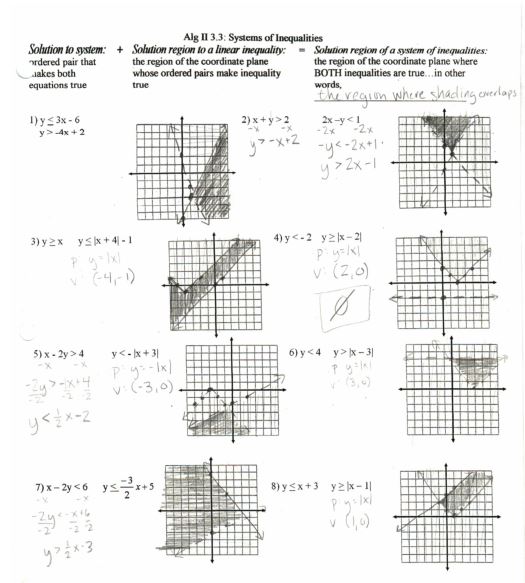File here. This is a fun worksheet to assign for homework:
Download here. You have to shade the correct portions to make a path!
Let’s stop here and have a quiz, eh?
File here. Then Linear Programming, which, to be honest, there are 1,000 things out there that are better than what I have. For example, Fawn’s Funky Furniture . It seems Steve had a similar idea and made a worksheet. Let’s all say hi to Steve!
So here’s an idea that sprung from someone scheduling an IEP meeting during one of my Alg II classes one year. I certainly couldn’t waste a day (since I would be seeing all the rest of the classes) and I certainly couldn’t leave them to “discover” linear programming with a sub. So I made these notes instead and gave that period filled-in copies.
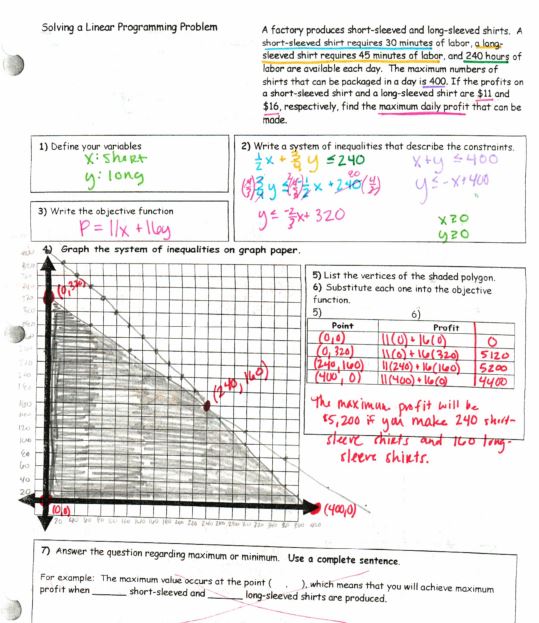
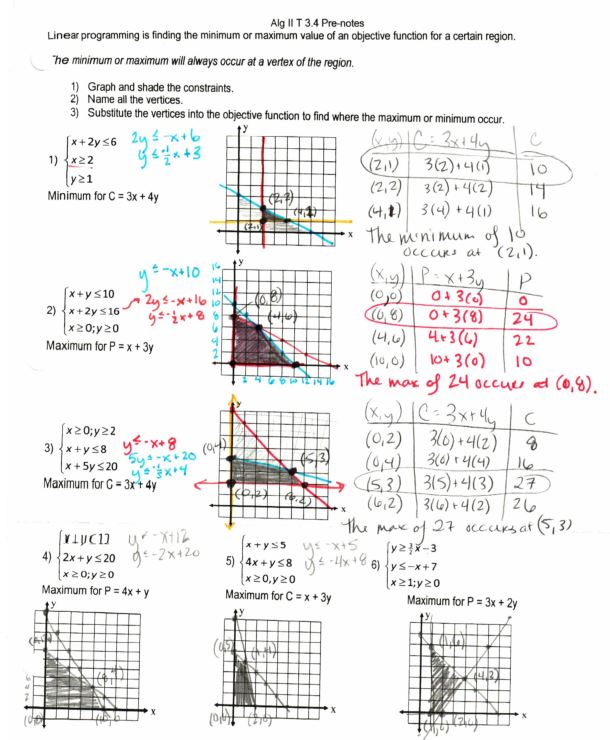File here. I’ve kept doing this as a day’s worth of notes because it makes the next day of introducing linear programming much less stressful! We’re not trying to graph more than two inequalities (new), finding possible max/min values (new), and plugging them in to find max/min (not new, but not common) AND read these really long word problems (scary), come up with constraints (new) and objective functions (new) all on the same day!
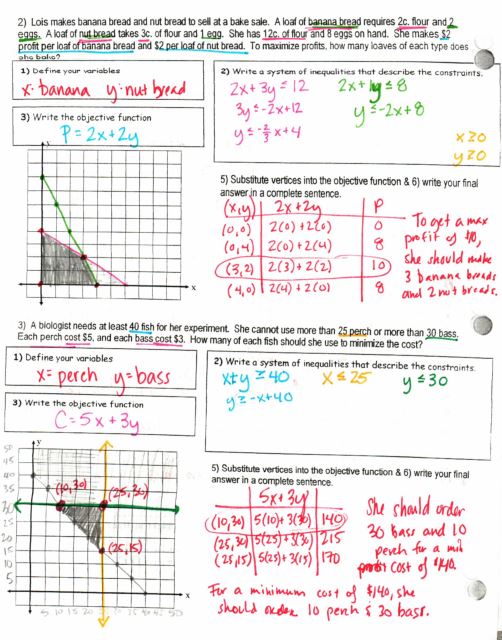
Here’s the next day:
And some more practice. I usually have them do this in pairs.
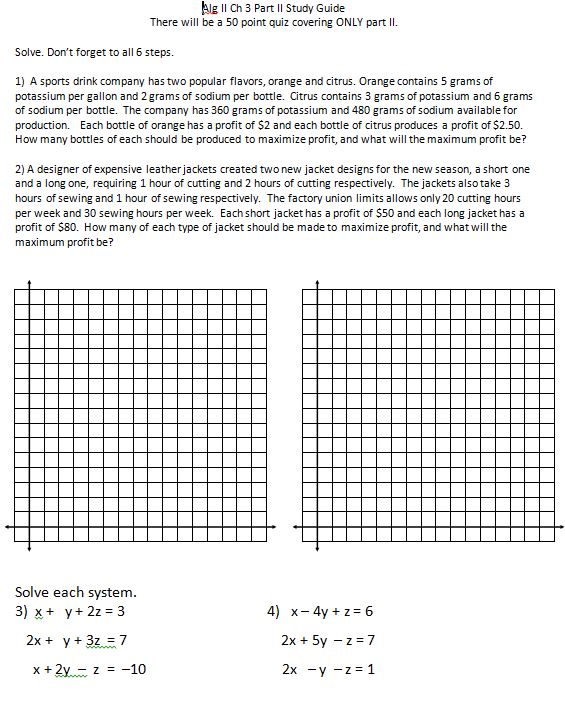
File here. Warning: #4 is a doozy! Sometimes I count this as a quiz (but I assist and they work together and I don’t tell them until the end), other times we solve some three-variable equations and have a bigger quiz.
I’d really like to find some linear programming problems where the answer isn’t just where the two slanted lines intersect. And by “I’d really like to find” I mean “does anyone want to provide me with.”
I feel this chapter is kind of meh. The first half they’ve already seen before and about half are great once we refresh their memories and half consistently struggle. Maybe this year it will improve because we’re going to do it at the end of all the different types of equations and focus on the graphing aspect a bit more. Basically I want to do what Jonathan did. Any other suggestions would be more than welcome. 🙂
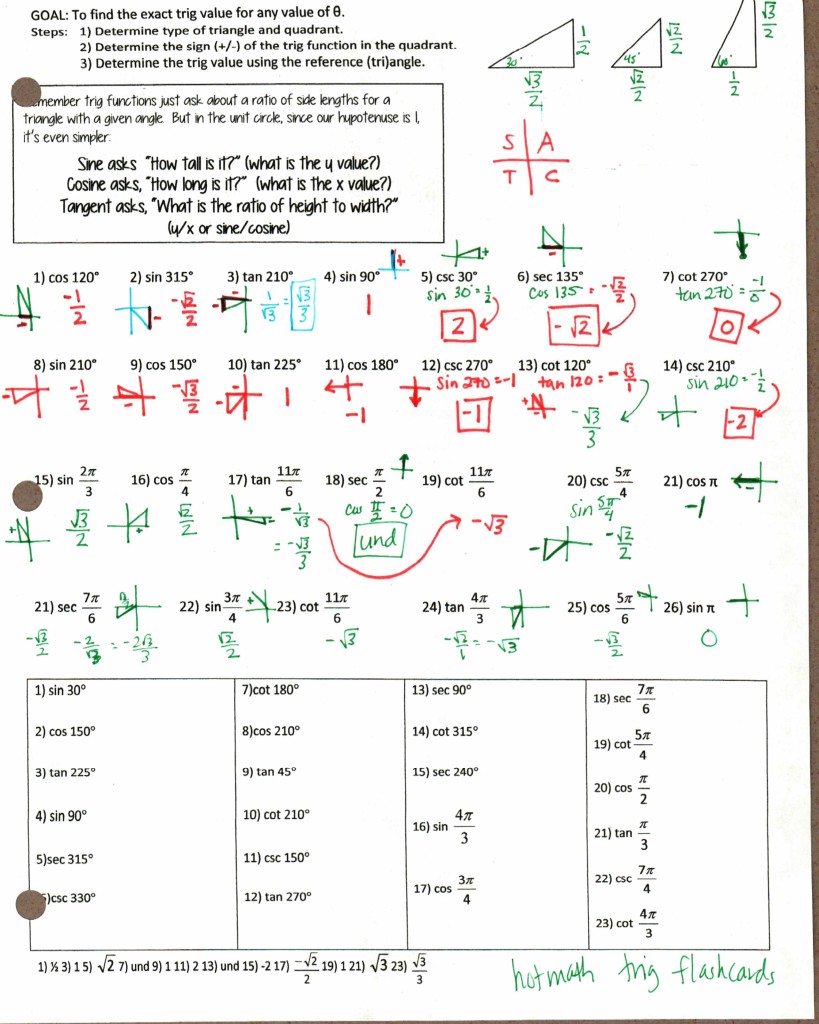
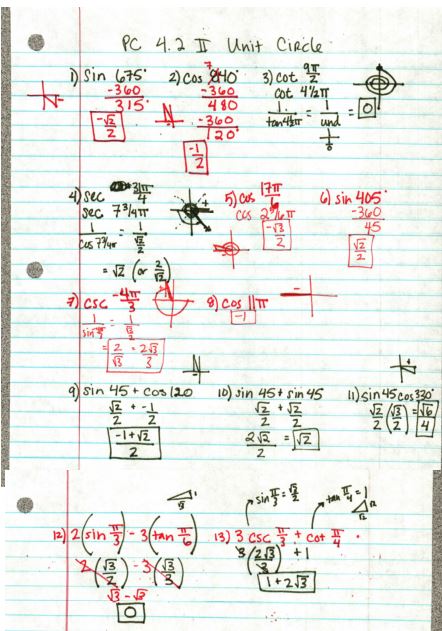
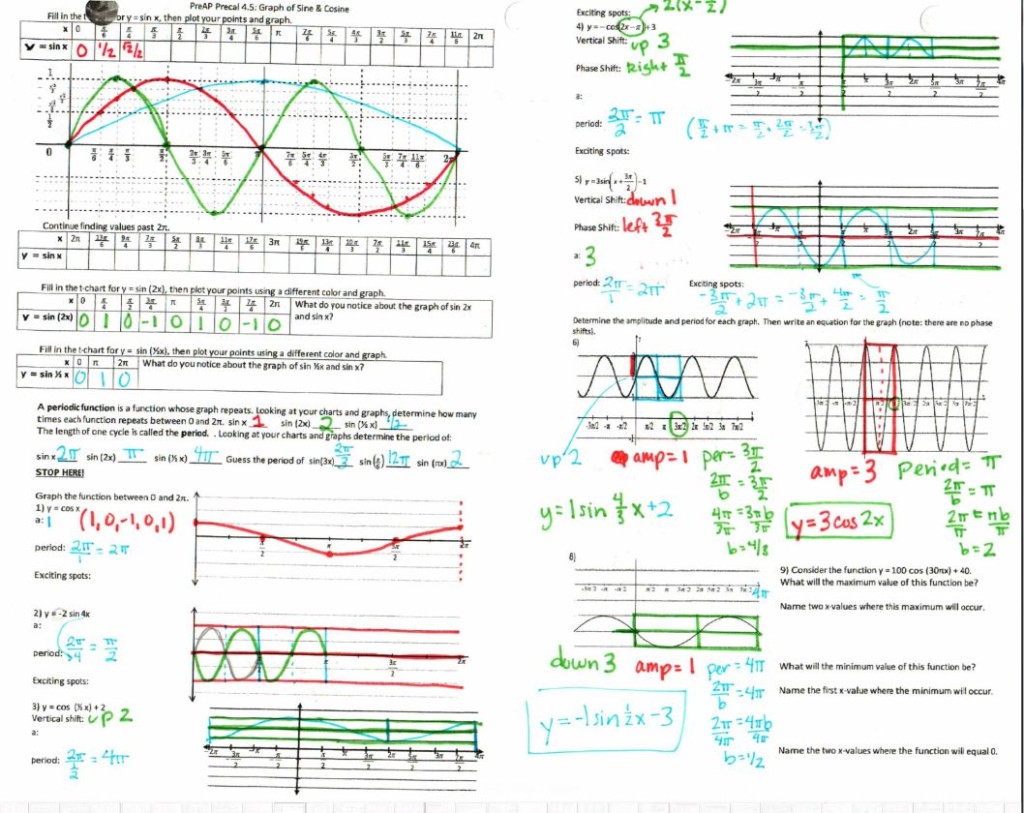
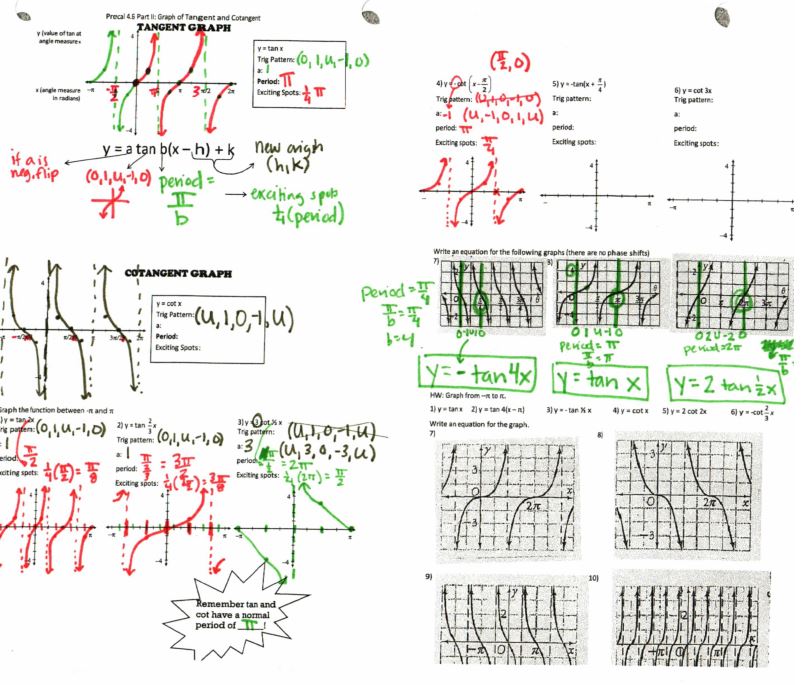
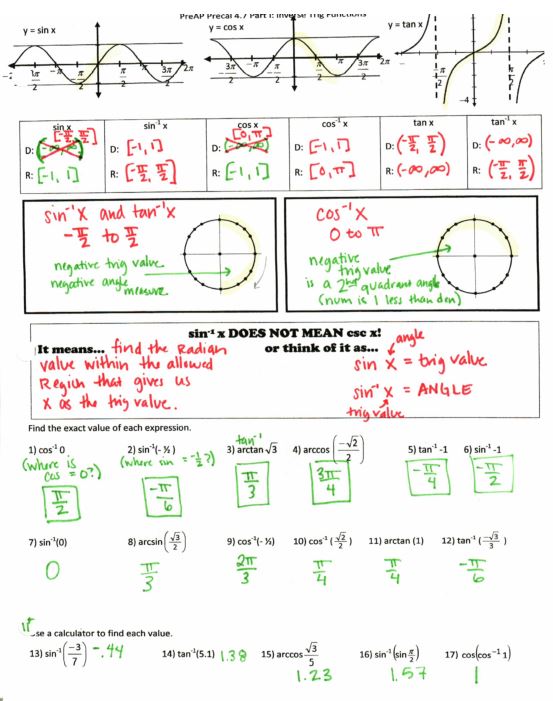
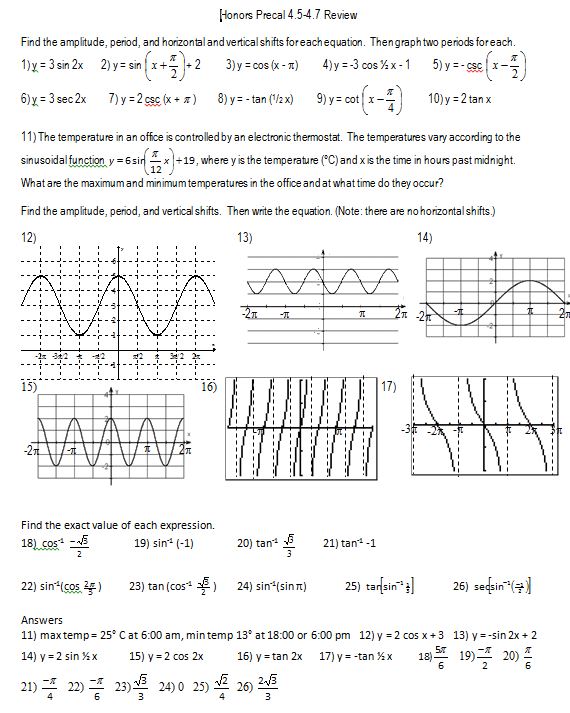
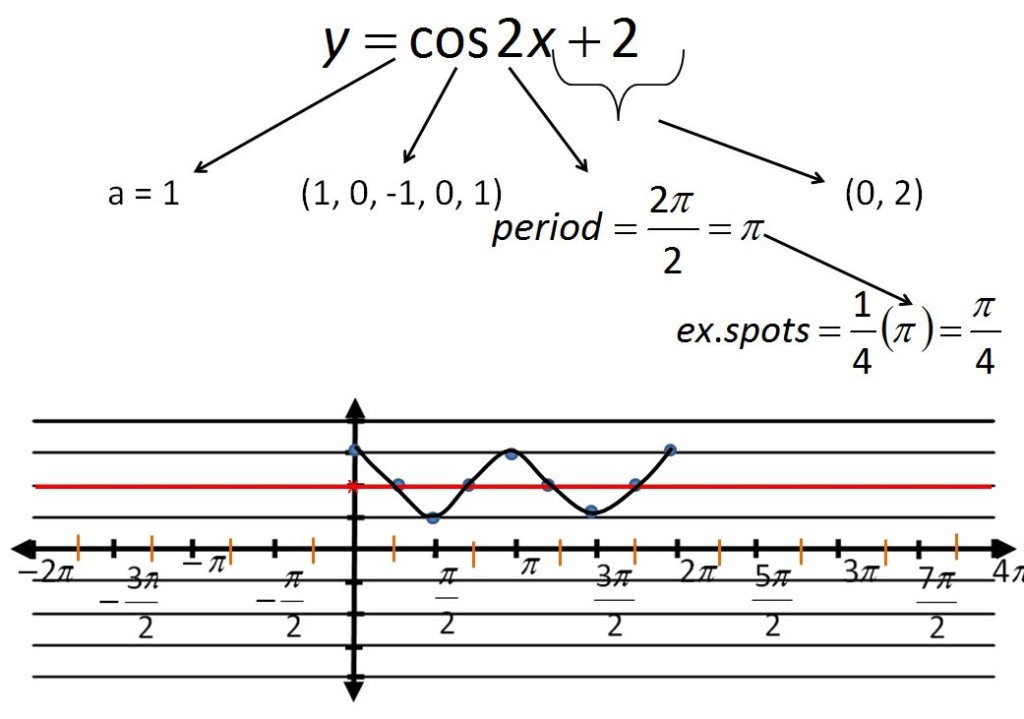
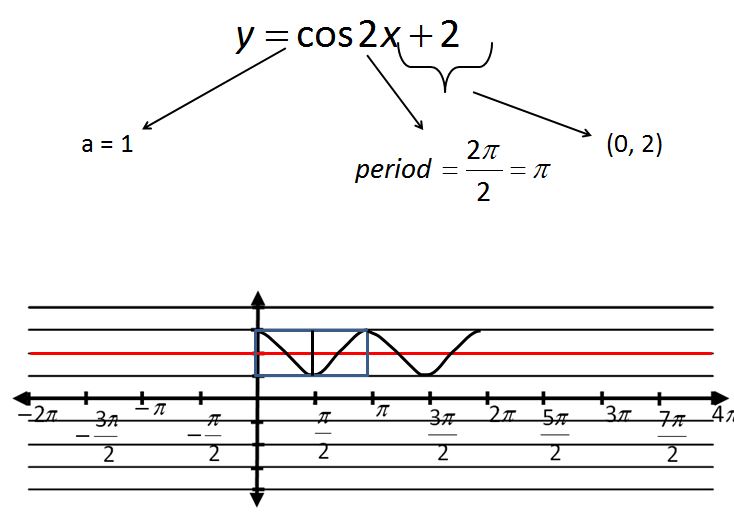
File here
