Permission: If you don’t teach Precal or Cal and (like me a scant three years ago), you have no idea what AROC or IROC means, feel free to skip this post and watch this award-winning animated short film about a dog instead. 🙂
The joy of teaching a mixed senior and junior class is that you miss half of them for all the junior AP tests and the other half for the senior ones, so I’m having to spread out my derivatives unit and come up with some activities that we can do on our own or in groups but still maybe learn something.
So here’s my take on using AROC vs IROC, page 1:
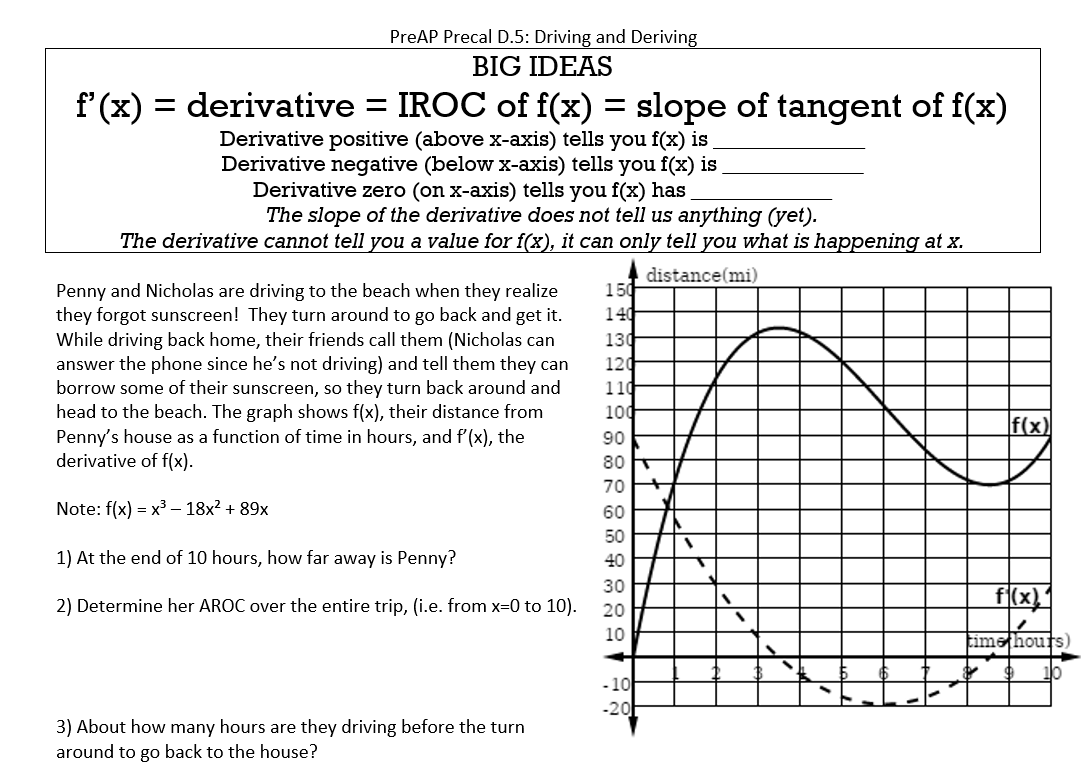

(File here) (feel free to steal this joke from my students: “Why did Penny and Nicholas turn around for sunscreen?” “Because they didn’t have enough sense!”) I now understand why textbook companies make the big bucks…it is hard to come up with a graph and derivative that make sense but still do-able mathwise! Looking at the derivative, Penny is pulling out of the driveway at 90mph then doesn’t get above 70 for the rest of the trip. BUT putting aside that little quibble, there’s actually lots of good stuff! Like the entire AROC for the trip is 9 mph. WAIT, what? Oh, look at all that time she wasted…basically from 1 hour to 8.5 she could have stayed parked at a gas station and accomplished the same thing. (Which made a light bulb go off in my head because it always hurt my head that AROC would be zero for that section but she can be MOVING with making PROGRESS!!) Also the negative AROC led to some good discussions.
Here’s page 2:

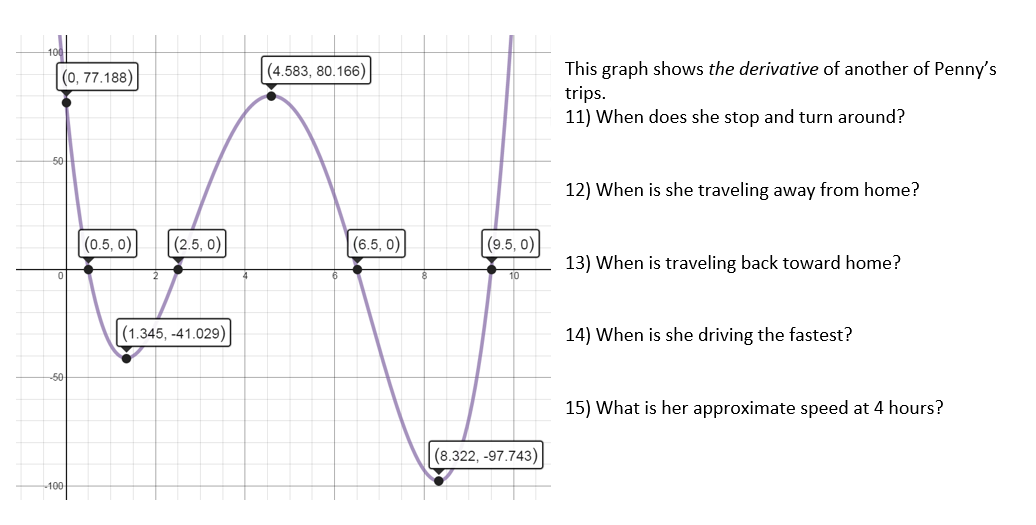
We don’t know the shortcut to derivatives yet, which is why they had such big space to work on that problem. I really liked #13 and #14 (ahem, the first 13 and 14) but I’m not sure if I should have scaffolded them more. I wanted them to create the equation of the tangent line and then use it, but that was difficult to get across. Most people just did speed x 10 hours. But the neat thing was, when I told a group they had to take into account that we were already at a certain distance at 1, they said, oh, so add that distance to the speed x 9, which tied in SO nicely to y=m(x-h)+k point-slope form of the equation!
As an added bonus, when they were done (it took about 1 full day + 15 minutes to finish, then 15-20 minutes to talk about everything including a preview of the power rule for derivatives), I copied this idea from Dylan and made it into a no-tech worksheet:
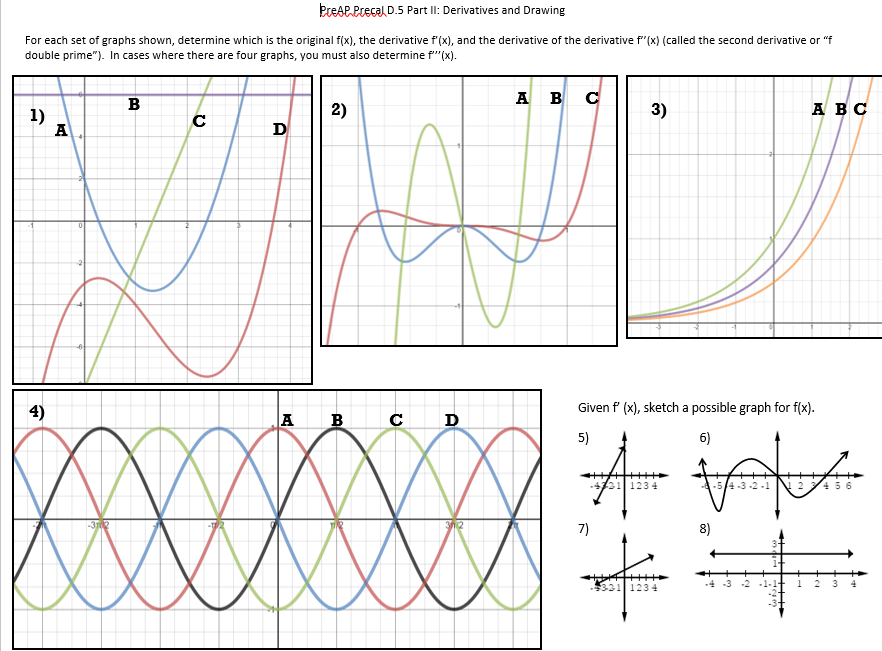
Making these reminded me how much I love making activities like this; I just wish I had more time to do so and that I was as clever as some of y’all at making great questions and graphs!
(so if any of you Precal or Calculus teachers have a great treasury of distance/velocity graphs or some hints on making pretty ones that are also somewhat realistic, please let me know! 🙂
Amy Zimmer
May 9, 2016 at 8:43 pm
Crazy these two weeks of mixture of students. I gave the students two assignments: If you are a Junior, it was a review for SBAC and for Seniors, a review for a College Math Placement test.
Next time I teach Pre-Calc, I will definitely hit more distance/velocity problems, this year my teaching partner had to finish early for hand surgery. I was focussing more on the messy Algebra and giving the students a reason for reasoning abstractly!