Due to mock AP exams and day-before-spring-break-ness, I decided to let my Precal students have two game days. With only five kids in each class on Thursday, I normally would just let them chill, but since I had all these fun games that Mr Craig is getting tired of playing all the time, I thought I would rope in my students into playing with me.

In case you’re looking for some good games, here are the ones we played:

Gameplay: Try to get as many of your pieces on the board while blocking others from playing theirs.
Pros: I think this was the favorite game. People were “calling it” as soon as they walked in the second day. Easy to explain, easy to play. Could get 3-4 rounds in each class, which meant more people could switch in and out.
Cons: Only four players, already lost a piece (made replacement out of a post-it)
Side note: This was also the game where the students helped each other the most. I refrained from telling them that the point of a game is to WIN.
Other side note: Seriously, you need this game in your house. Now.

Gameplay: Try to move the maze to allow access to treasures, but the maze changes on every turn!
Pros: Lots of deep thinking, fun strategy, “this is the game that can ruin friendships,” also players went from worst to first and back again throughout the game (instead of one person running away with the win).
Cons: Long game play (took almost the whole period with 4 players), only four players, sometimes you get stuck for a long time in a frustrating location

Gameplay: The lovechild of Scrabble and Set. Play your cards crossword style, but each characteristic must either all match or all differ in a line.
Pros: LOTS of reasoning and strategy!
Cons: The rules are a little bit dense to start with. Students had to keep referring back to “what makes a line?” but when I came back towards the end of the game, they seemed to have gotten the hang of it and enjoyed it. Takes a tabletop surface to play (I put a big group whiteboard over four desks to play on)

Gameplay: Lay out 16 cards and try to match hoops and dots by rotating or reflecting.
Pros: This was the second-most popular game (students wanted to borrow it later in the day). Easy to learn and very quick game play.
Cons: Becomes a bit hectic with everyone calling out swish at the same time, it is hard for the dealer to have an even chance with the rest of the players (or at least I’m going to use that as my excuse)
So I would say Game Day was a hit and at least slightly more mathy than watching Pixar Short Films collection.
Do you play games in your classroom? What are some of your favorites?


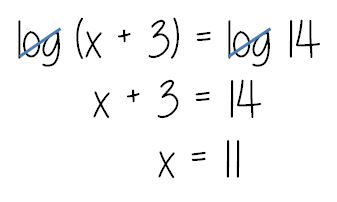
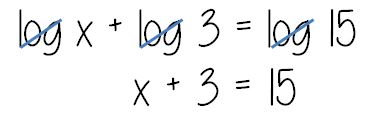
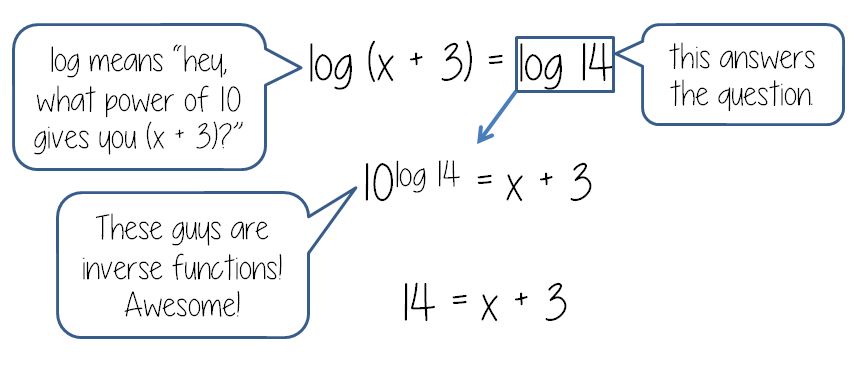

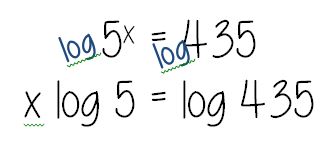


.png/revision/latest?cb=20130322232649)

