(If you want more Algebra II files and for FAQs (including fonts), look here!)
Part of switching up the order of Algebra II involved moving up solving quadratics (which used to be Chapter 5, after equations, lines, systems, and matrices). I like how nicely this worked with Unit 1, however, I definitely needed to spiral more through the year, I wasn’t very good at making sure they saw all these different types of equations again through the year. But here’s how solving quadratics went!

(file). This is basically how every lesson went this year: “Oh, man, I’m going to make the COOLEST note-taker-maker and it’s going to have SO MANY CONNECTIONS and it’s going to be awesome!” and then about 20 minutes into class…

Usually it was a case of “Trying To Fit An Hour’s Worth of Class into Forty-Seven Minutes” but other times I think I aimed too high, or didn’t plan for so much review, or maybe it was just “First Time to Teach a Lesson Never Goes Well” issues.
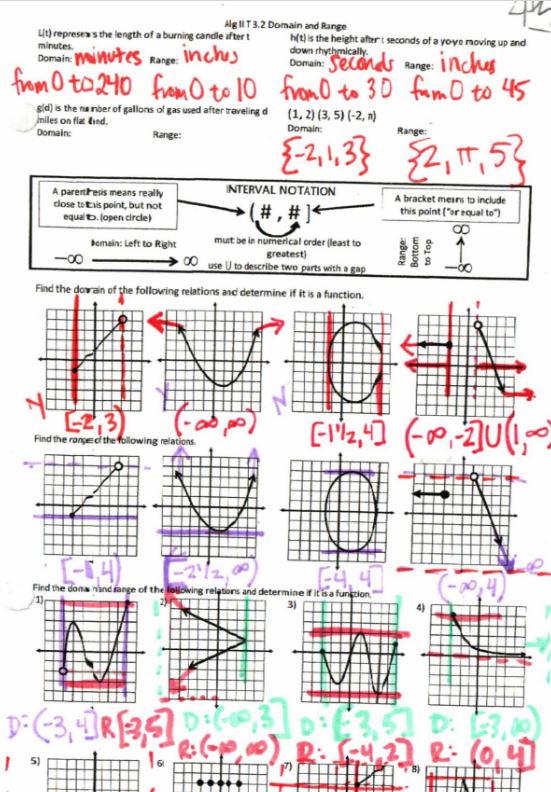
Anyway, as you can see, I didn’t get finished with my connections the first day, but I think you can appreciate where I was going with it-my students always seem to think “factor” means “solve” and “simplify” means “factor” and such. And also they forget that they can solve quadratics without a linear term without factoring, just like they did last chapter! (Although I will admit I often get into factoring-robot-mode and forget that, too!) I think with three minutes left in the class, I decided to focus on factoring/simplifying for the moment, then go back to solving.
The next couple of days were spent factoring trinomials by guess and check. (Hey, spell-check, “trinomials” is a word and I did not mean “binomials”). We used whiteboard for easy guessing and checking. You can read all about it here! If you’ve always been wary about guess and check, I ask you to go give it a read and maybe try it out next year. It’s not your momma’s guess and check!
[Updated 7/9 to add the following picture] Ok, so I bet you DIDN’T go and read all about the cool guess and check method, did you? Well fortunately for you, Susan () tweeted me a concise picture of it!

Thanks for the great example, Susan!
Hey, for the rest of y’all, want some homework?
(file) Or maybe some group speed dating cards?

(File). As mentioned, I may have gotten lazy and just handwrote the answers on the back of each. Perfect is the enemy of the good, eh?
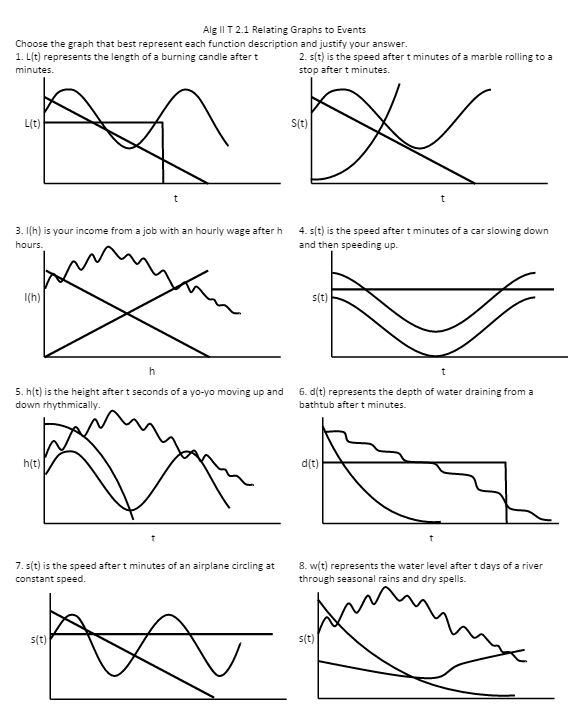
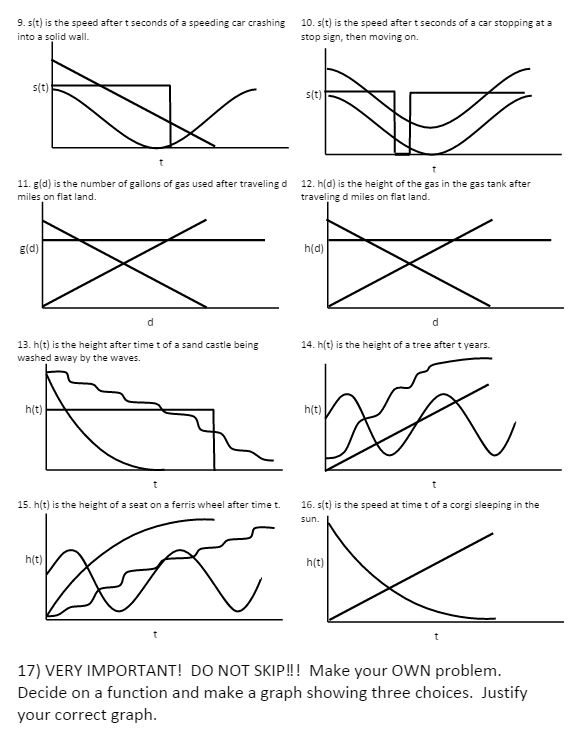
Ok, now back to solving quadratics! News flash: I use a lot of terms that I just think students should know by now. But they don’t! Even if I didn’t do it formally each time, I started each equation/function intro with “how do you spot it in the wild?”

Those weird symbols meant we asked ourselves HOW we were going to solve it before we actually started solving.
(file). Make sure you play the “Guess Which 2 Numbers I Multiplied Together” game that I stole from someone on the #MTBoS (please tell me if it’s you!). Start with 10. They’ll chose 5 and 2 and then 10 and 1. Nope, it was 20 and 1/2! Tell them you’ll make it even easier…they just have to name ONE of the numbers. Give them 20. Someone will say 1/2 and 40. Nope! 1/5 and 100! Then say maybe it will be easier with a smaller number, like -1. Nope, it was 1/pi and -pi! Then finally give them one more chance…name one number out of 2 that I multiplied to get zero. TA-DA! And that’s why it’s the Zero Product Property, kids, and not the “0 or 1 or 10 product property.”
And why we’re blowing minds, let’s talk about imaginary numbers!

(file) Truth: I just introduce imaginary numbers as a way to solve a problem we couldn’t before (I start with the story about the caveman owing more sheep than he had, so he tried splitting it (fractions), but then he still owed more sheep (negatives) then bring in Pythagoras and the madness of irrationals and how we end up making/discovering new categories of numbers in order to solve previous unsolvable problems. If I teach this again, I’m also going to use the tidbit from The Thrilling Adventures of Lovelace and Babbage about how one of her tutors didn’t believe in negative numbers (and this was in the 1800s! Not that long ago!)). I don’t get into doing operations with them, or rationalizing them, or even the cool power pattern unless I have a few random days free later in the year.
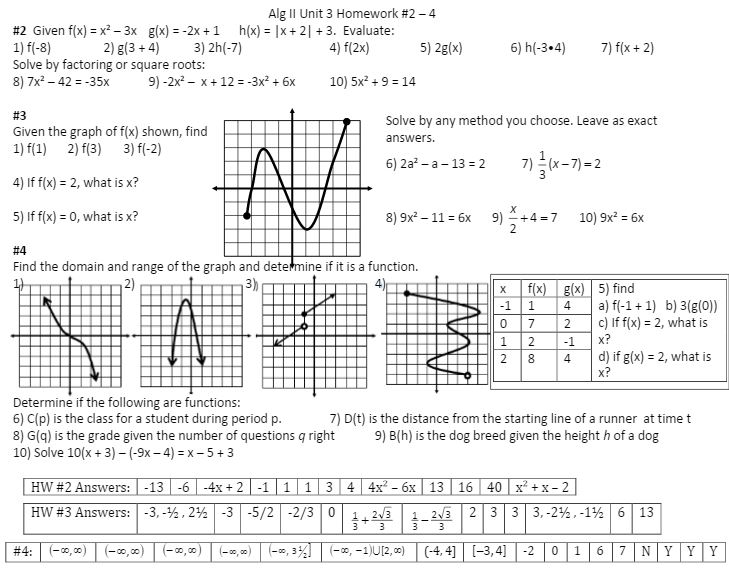
Then it’s time for a big ol’ bag of practice:
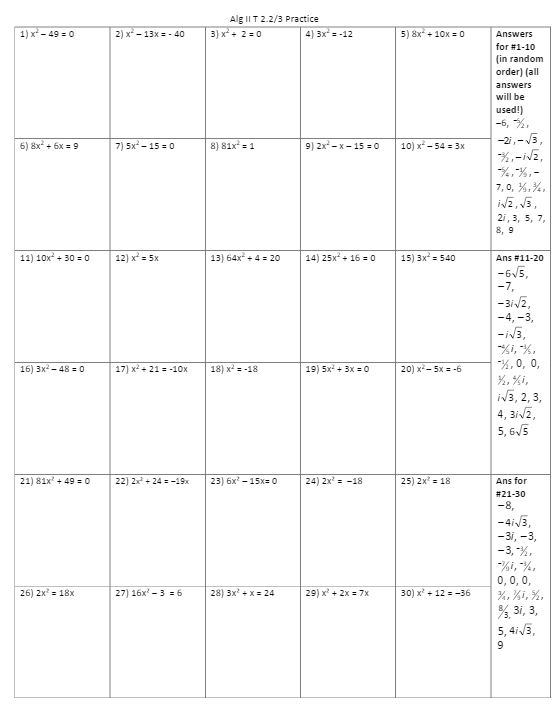
(file) Another truth: Not every single practice activity has to be filled with razz-ma-tazz. This has some nice self-checking built in, and I just wander from group to group. I’m in the camp that sometimes you just have to do a lot of practice and I’d rather have them spend all period in groups working on all of these problems, then spend half the time trying to do the practice and play a game, then not finishing, then just copying the rest from their partner. Not to say I don’t love a good activity, I’m just sticking up for the worksheets because somehow worksheets started to be shorthand for bad teaching and I don’t agree with that. And I’m giving you permission to NOT spend hours converting a perfectly passable worksheet into an (awesome) activity and maybe watch Halt and Catch Fire instead?
Ok, let’s get back to something we can all agree on: the quadratic formula!

(No file, but there is a page 2) Well, except we don’t all agree on how to write it. Notice the beautiful splitting into 2 fractions (and you can still sing “all over 2a!” during pop goes the weasel) which is a masterful tip I learned from Jim (@mrdardy). (We do have to talk about recognizing the right answer during multiple choice tests, though).
Am I the only one that talks about “pretty” numbers? And gross decimals? I am? I’m cool with that.
Hey, remember what I said about worksheets? Yeah, here’s one that is based on Amy’s great activity. I feel so guilty-like I just undid millions of MTBoS tweets by turning an activity into a worksheet. Does it help if I told you they work on this in groups? Please don’t kick me out of the MTBoS; my TMC16 airfare is non-refundable!! I mean, check out the directions…they still have to choose which 5 to use the quadratic formula on! There’s thinking, not just rote practice! I promise!

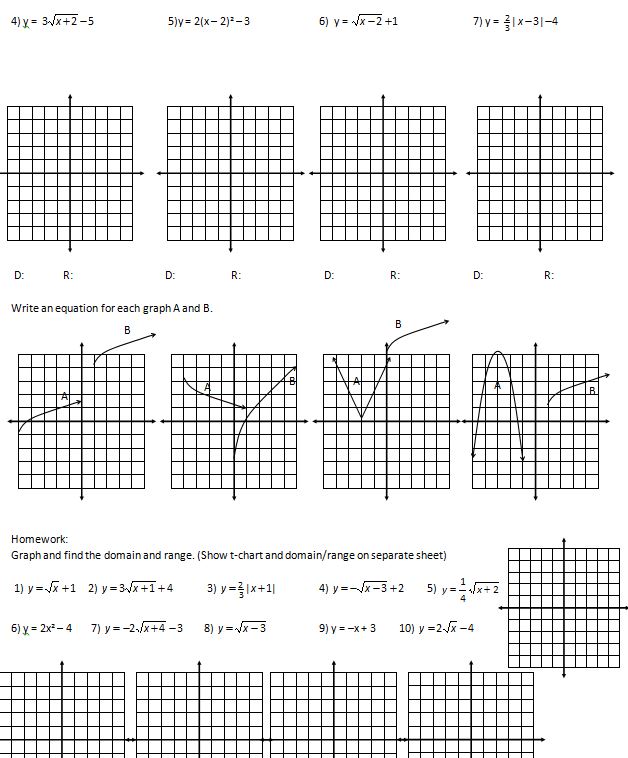
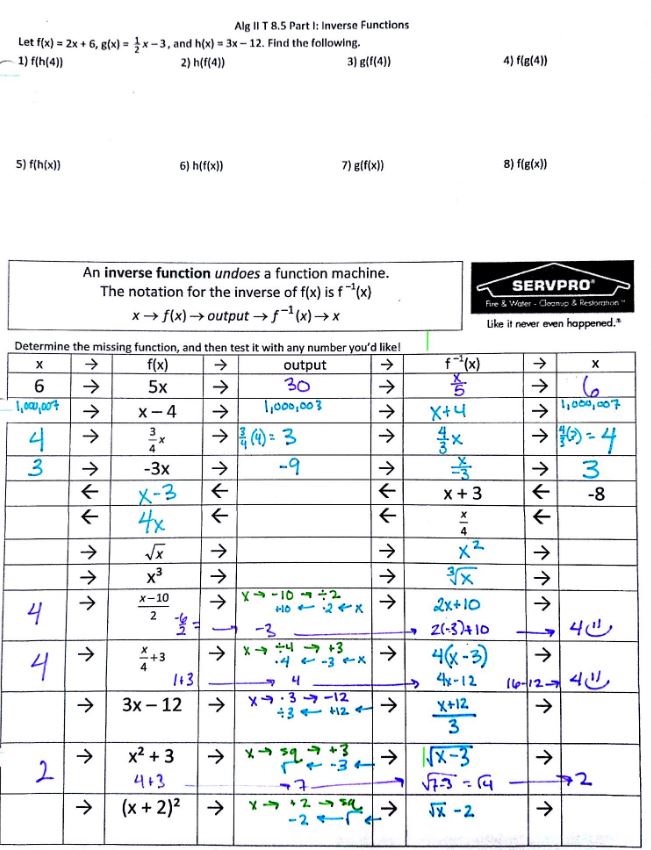
(file) Hey, you know what this chapter needs? Some radical equations!

(No file). Ok if there is one thing my Algebra II students left knowing this year it’s that (x – 5)^2 means (x – 5)(x – 5). A few dramatic gasps and some fake tears over the dead puppies the first few times someone tries to distribute the exponent and they seemed to have remembered it. Of course, I’ve done the same thing in other years and it never worked, so YMMV.
You know, I think we may need some more group speed dating:

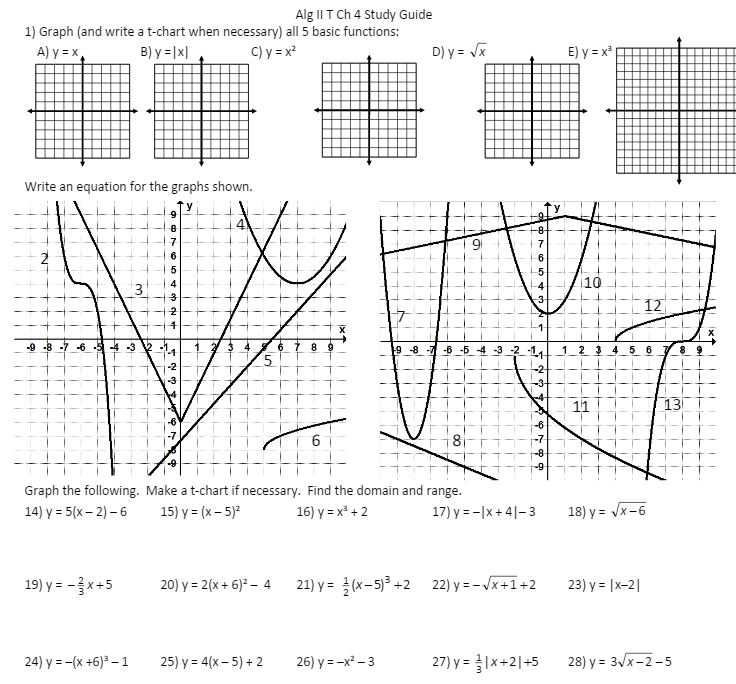
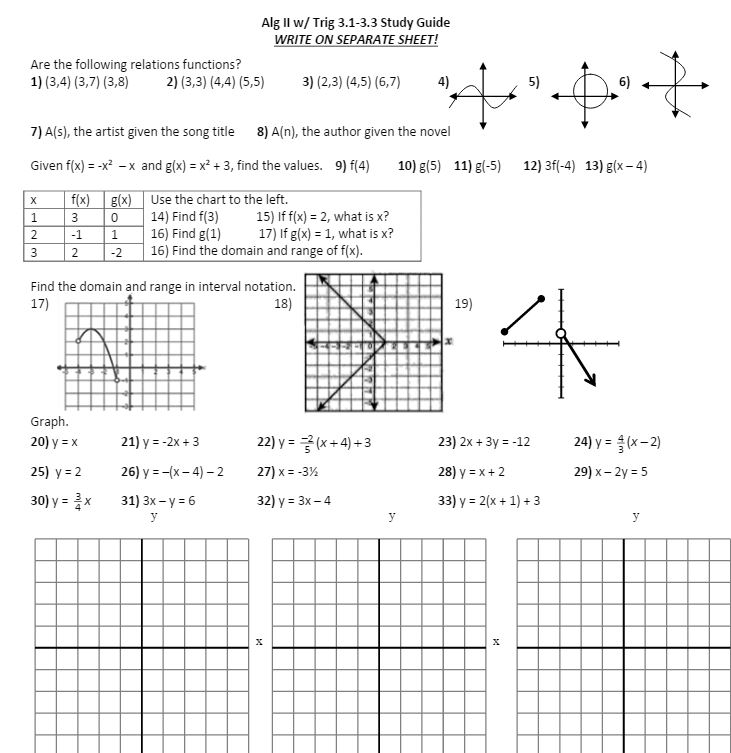
(file here AND it included answers!) Then it’s finally study guide time!!

(file) And if you’d like to hear the beautiful sound of my voice explaining 31 different quadratic problems, here are the showme videos of the study guide: #1-11 #12-27 #28-31.
Whew! That’s a lot of quadratics, my friend. Hope you found something useful! As always, feel free to leave a comment or tweet me if you have any questions or found a matho!





























































 But inside I’m really:
But inside I’m really:

 (
(