Monday I spent a couple hours falling into the #MTBoS trap of lesson planning: having so many shiny pretty ideas that I can’t decide what to do! I was trying to figure out how I wanted to start my exponential unit for PreAP Precal. Yes, they’ve seen it before, but I didn’t think they had a concept of EXPONENTIAL BEATS EVERYTHING (I know I really didn’t until my [REDACTED] year of teaching math.) So this is what I came up with:
You just started a new job. Pick the best salary option and be prepared to support your opinion:
Option 1: $50,000 a week, increased by $5000 each week.
Option 2: $100 times the square of the number of weeks you have been working (I didn’t really know a better way to describe this?)
Option 3: Start at $10 a week, increase by 10% each week.
It was a weird day yesterday with some classes half-full due to class meetings, plus I had some tests to go over, so we only had about 25 minutes to work on it. I let them have 10-15 minute to discuss in their groups. Many people started with a table, which is quite deceiving at the start. A few groups finally asked, “how long are you working there?” To which I replied, “That’s a good question, how long are you working there?”
Most decided to focus on one year, and thus chose option 1. A few ventured out further and chose option 2. (Maybe next year I’ll make so option 2 overtakes option 1 just before year one instead of just after?) Most could not figure out an equation for option 3 (which didn’t bother me, especially when they haven’t seen exponentials in over a year), so just crossed that one out immediately based on the first few weeks.
After each group gave their reasoning, we worked out a table on the board, starting with 1, 2, 3, 4, 5 weeks, then figuring out the equation for each week. I then gave each group a time frame-1, 2, 3, 5, 10, or 20 years and had them figure out the weekly salary for each option. The bell rang right in the middle of posting the results, but we still had fun talking about making $10^22!
Today I showed them the graphs in desmos and we talked a bit about them:

(Desmos file here) But I think we FINALLY got the power of the exponential when we put it in table form:
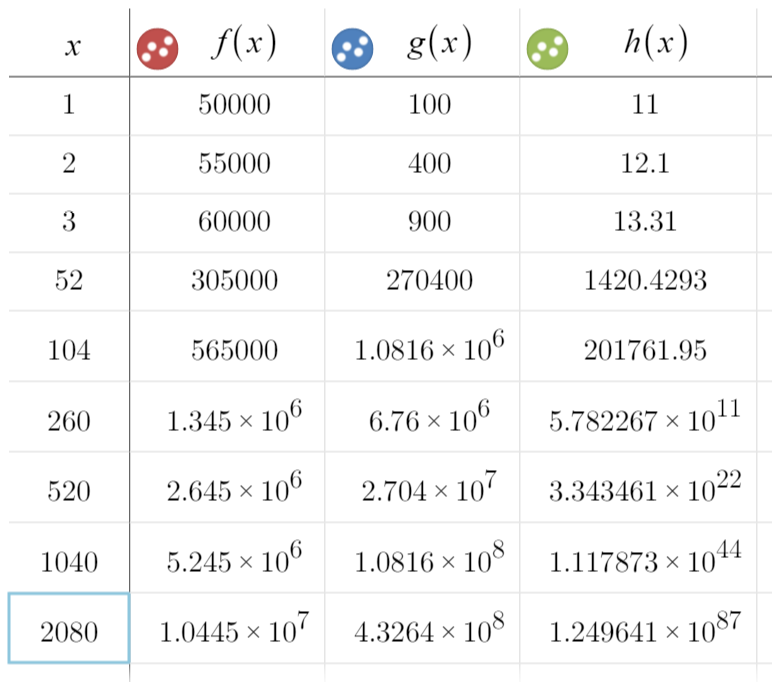
I mean, look at how slow both the linear and quadratic are growing. 10^8 after 40 years? That’s not even worth getting up in the morning for! I also wrote out the final numbers on the board while they were working on the next task, using all 87 zeros.
Yup, I think they will say that exponential will win every time now. 🙂
As we were working on it, I thought of a lot more things we could extend with:
- Figuring out the time to switch by solving a quadratic (option 1 & 2) or by using technology–either Desmos or using Excel?
- Have them write an actual recommendation of which salary to chose and why.
- For the first couple of years, students were wondering if making so much at the beginning would make you have more money at the end of the year with the linear. What a perfect way to bring in area under the curve! Especially because they could actually calculate the linear function’s area with just one trapezoid, then I was thinking just to use the integral function on the TI for the other two.
- Of course it could also be a nice lead-in to logs: when will each salary hit $100,000? $1,000,000? $10,000,000? (Also nice to look at graphically!)
So this post is serving as my reminder to myself to devote some days to this next year, and try to do some of these extensions. But if any of y’all want to try it out and make it awesome as you are wont to do, please do and report back! I’ll be chillin’ with my cool $10^87.






