[More files and FAQs on my Algebra II files page!] One big change I made in Algebra II was making an entire graphing chapter. Usually, we would learn a function, solve it, then graph it, repeat. Now, using Jonathan’s model, they all got mushed together in one unit, which actually really helped them with (a) things that are similar with all the graphs (shifting, stretching) and (b) things that are different. It also solved the issue that I had before where if we were in the quadratics chapter, they would just write y = (x – 2) + 6 for the equation, leaving off the most important part! Now they realized why that was so important! I was reeeeeealy pleased with how well the students did on this unit. I needed to keep spiraling back to these through the rest of the year, though, because when you graph all at once it’s a long time before you graph again!
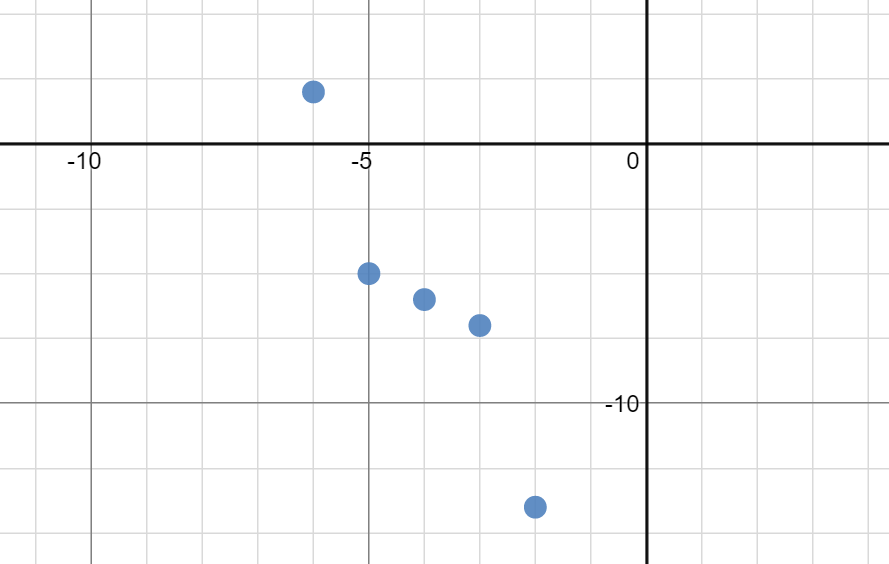
When we last left our intrepid reporter, she had just finished translations of linear functions, so now we’re ready to jump into absolute value. The first part that they did mostly on their own:
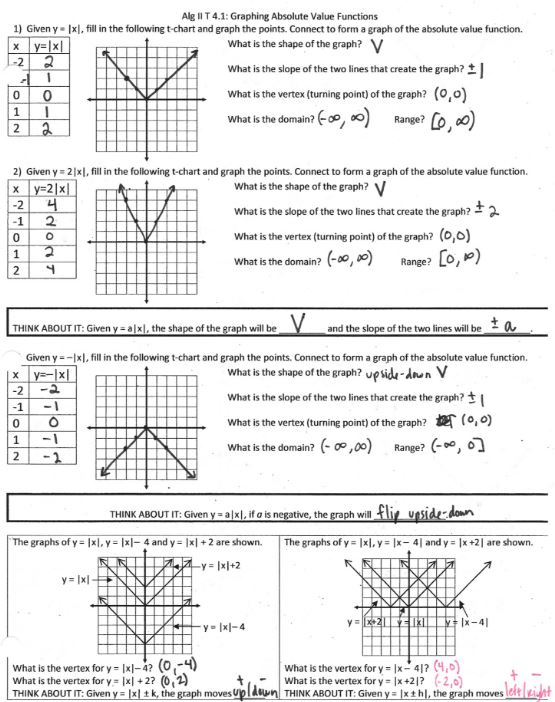
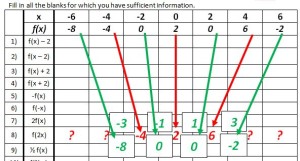
Second part where we made sure everyone was on the same page: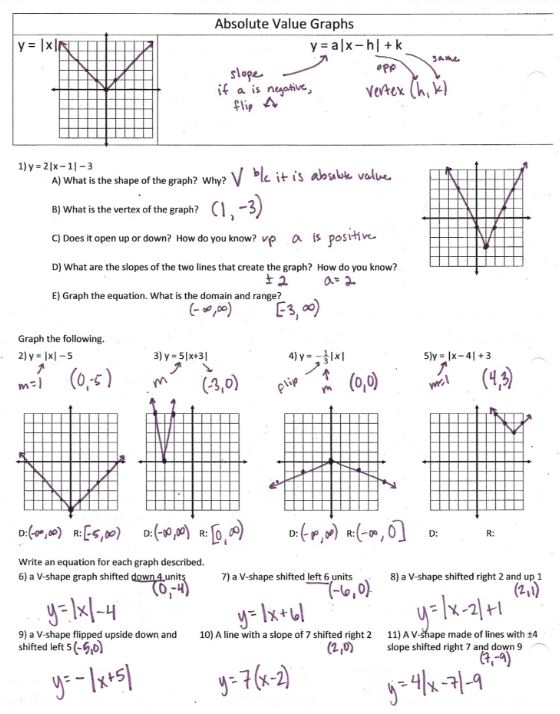
(file and a practice WS file) I REALLY liked those questions on #1 that I stole from some worksheet; you’ll be seeing them for the rest of the chapter! Like on the quadratic NoteTakerMaker!


(file and homework) Again, we were just focusing on graphing by translating in this chapter. Let’s try translating some square root functions!

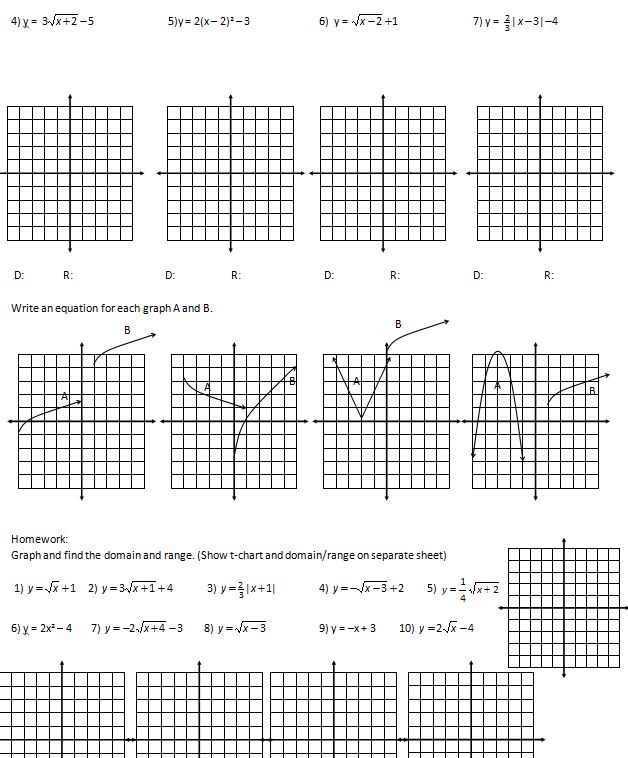
(file) And then it’s time for some John Travolta!

(file) This was the last function we were going to study, so we spent a day doing a Desmos “Match My Function” Activity Builder:

You can find it here. I think this was the first activity builder I made all by myself, so it’s not very elegant (it was before hidden folders so I had to monitor students not scrolling down to the answer!). I also had some students say it was too easy to just use sliders until it matched, so next time I would definitely add some Desmos-style questions like “Here is Addison’s (wrong) equation and graph. What would you tell her to correct so it matches?” and “How would you explain to your friend how to move a function left or right?”
Then a group speed dating day:

(file and yes the graph answers are included!) Some sort of dry-erase graph is a must for this activity so partners can see work! If you don’t have individual graphing whiteboards, take Tina’s (@TPalmer207) suggestion of buying a pack of job ticket holders and printing off graphs to put inside.
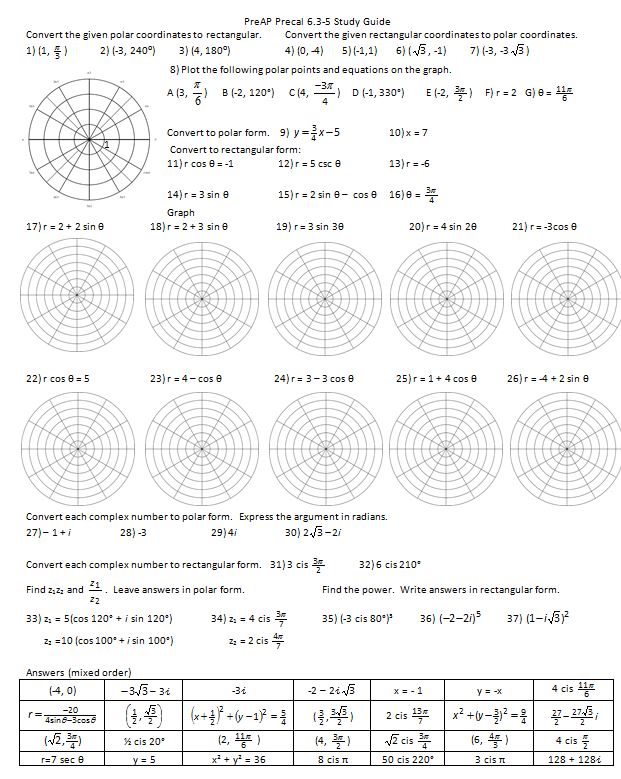
Then it was study guide day: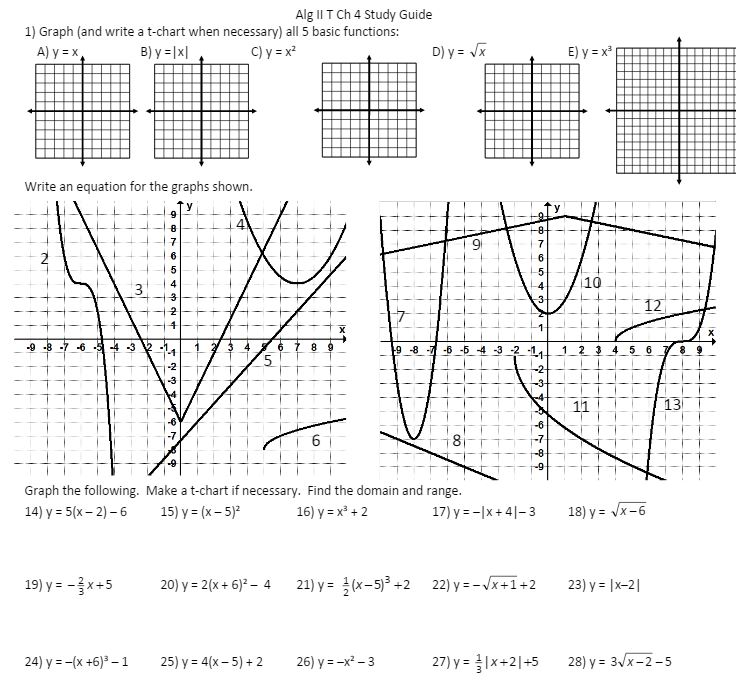
(file and video key part 1 and part 2) As I said at the beginning, for the most part the score were GREAT on this test! Was it because we ended up going pretty slow through this unit? Or because they had graphed most of these before in Algebra I? Or because all the graphs were together? I don’t know the reason, but I will definitely put this portion of restructuring Algebra II into the “win” column!