Alternate title: A Week in the Life of an Algebra II Teacher
Like a parabola, my quadratics graphing unit started off going downhill fast, then made an unexpected upturn at the end. Warning: this post is also to remind myself how to make it better next year, so there’s a lot of second-guessing and rambling.
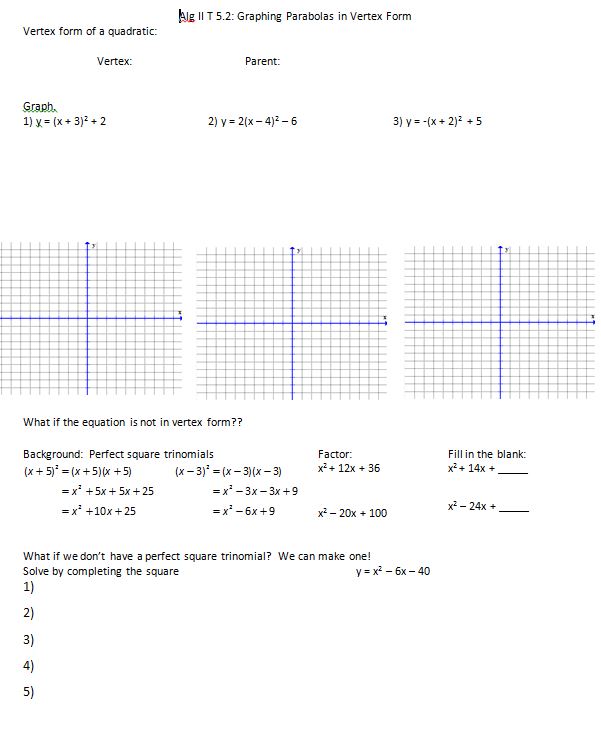
I knew I wanted to talk about the three forms you see when graphing…standard, vertex, and intercept/factored form. I also needed to talk about completing the square and wanted to throw some applications in there. So here’s how it went:
Monday: Gave them this investigation activity that I think I stole from a book. Thought, “hey, they liked investigating absolute value graphs with the calculator, so this should go well.” Out of the mouths of babes…

 Files: First page, Second page
Files: First page, Second page
After handing back and going over tests, we had maybe about 30-35 minutes to work on this in class. If I had planned this earlier than Sunday night, I could have tried to get the computer lab and used desmos, but as it was, it was kind of difficult for them to figure out which graph was which. (yes, we talked about the trace button and then they all put the y-intercept as the vertex on #2 because that’s what x- and y-values came up on #1.). They finished to the first chart on the second page and I told them to finish the rest for homework. Well, since the rest involved doing something that was not specifically taught step-by-step in class, they all gave up.
Tuesday: Hey guys, let’s talk about what a college-ready course is and is not. I’m sorry you’ve been spoonfed math for the last ten years. I’m sorry you think you can’t do this. I’m sorry you’re so scared to fail you won’t even try something. I’m sorry you didn’t even realize that just like you did for the last FIFTEEN graphs, you could have put your equations in your calculator and checked them. I’m sorry you think I’m the worst math teacher in the world, but you’re stuck with me until May so deal. I discussed finding the a value given a graph a little bit and repeated this for at least two questions on the bellringer for the rest of the week*. About 25% could write the equation correctly on the quiz.
*Side note: Maybe I’m doing that part wrong. I used to do the ol’ plug in the vertex and another point and solve for a, but that always turned into:
y = a(x – h)^2 + k
3 = a(5 – 2)^2 + 6
3 = a9 + 6
3 = 15a!!!!!!!
Plus I wanted to make a connection about how the a affects the graph, because I don’t think they see the connection between “solving this equation for a” and “what does that mean about our graph?”
So I tried this way:
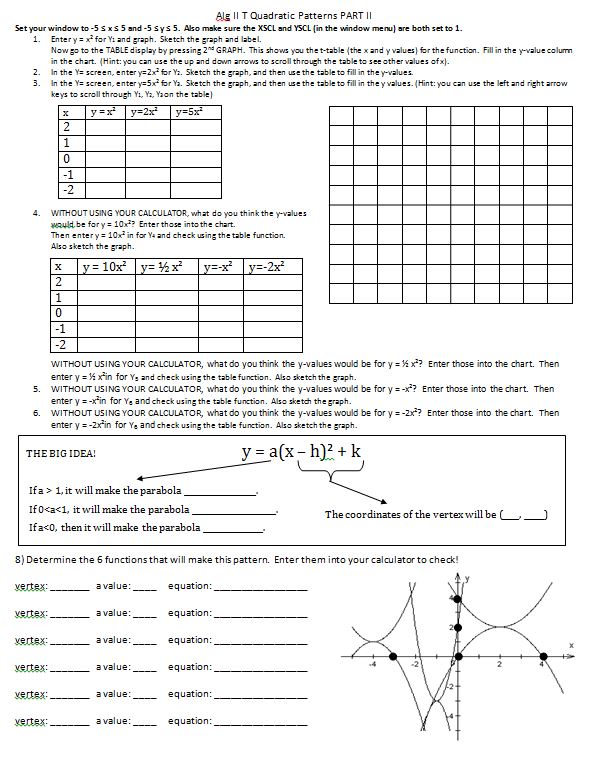
To graph, we make our standard t-chart and multiply the y column by a:
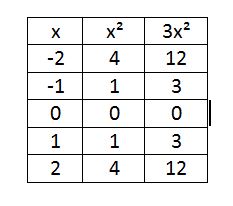 So let’s solve this as a puzzle, let’s say in my graph I can tell that when I move over 2 from the vertex, I go down 8:
So let’s solve this as a puzzle, let’s say in my graph I can tell that when I move over 2 from the vertex, I go down 8:
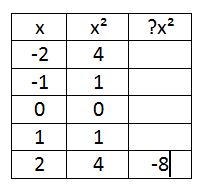 What would we need to multiply the y (or x squared) column by to get that value? I personally loved it, as you can tell by the % correct, the students not so much. I think maybe everything was a bit rushed and we should have worked on it after the following instead.
What would we need to multiply the y (or x squared) column by to get that value? I personally loved it, as you can tell by the % correct, the students not so much. I think maybe everything was a bit rushed and we should have worked on it after the following instead.
End side note, returning to Tuesday’s lesson…
We formalized graphing in vertex form and completing the square using this note-taker-maker.
(file here) I was impressed with how well they were doing. Probably 97% got vertex form right (2 or 3 still multiply the x’s by the a value instead of the y/x squared), about 80% got completing the square completely right, 17% silly errors, 3% well, that’s an interesting take on completing the square.
Wednesday: Oh, so it’s going well? Hahaha, let’s fix that. Applications!
(file here) Wednesday is our short period (47 min versus 52 min on T/R) so I didn’t get to show the Vomit Comet video (especially when you factor in the 5 minute lead time I need to open a web browser on my computer). One kid was really into it and started asking all sorts of science-y questions that I had to come home and ask Mr Craig about, so that was kind of fun. We had time to do get through problem #1 in most classes.
Thursday: Finished up #2 as a class, omitted #3, then let them loose on their VNPS (vertical non-permanent surfaces AKA whiteboards) for the rest. And every single team found the vertex when they asked for the number of tickets sold in 2005.
Me: Was that when the maximum number of tickets were sold?
S: Yes?
Me: How do you know?
S: Because we used -b/2a
Me: What does that tell us?
S: The x-coordinate
Me: Of what?
S: The vertex
Me: So what does it tell us?
S: When the max was sold
Me: Did you get 2005 for the x-coordinate?
S: No
Me: So do you think the max was in 2005?
S: Is it because we forgot parentheses in the calculator?

Even though it was a long period day, some students still had to finish a couple for homework, including the mixed graphing at the bottom. Let’s just say my idea to throw in y = 2x-1 was not met with enthusiasm. Or knowledge of a line. (I may need to use @stoodle’s function spotting guide with them!)
On the test, most students were able to find the maximum and when the object landed. However, on the test the x’s represented feet away instead of seconds and that threw a lot of kids (as in, many students told me the max was the x value and it occurred at the y value). Something to focus on for next year–maybe try it without numbers or solving first? Maybe talking about what f(6) = 15 would mean in context? I also found myself using the reverse of Sam’s phrase of “turn what you don’t know into something you do know”: “how can you use what you do know to find what you don’t know?” (Another side note: we were doing the same idea last week in precal with parametric equations and that idea came in very handy! Know the x? You can find t! Then you can use t to find y!)
Friday: One day left before study guide day. I wavered back and forth a lot on what to cover. The other Alg II teacher wasn’t going to be able to cover factored form, so I thought maybe just focusing on standard. But we already covered finding the vertex and converting to vertex form. So I did a little searching and found this awesome foldable from High Heels in High School (oh, I remember when I was young and could wear high heels every day. Those were good times.). I ended up modifying it a bit by (a) not making it foldable and (b) changing up “axis of symmetry” to “how to graph.” Here’s how mine ended up looking:

Then I found this TOTALLY AWESOME activity from the Mathematics Assessment Project that involved matching equations in the three forms to graphs (I skipped all the rest of the stuff in there and focused on the dominoes). The dominoes print nicely 2 to a page, but next time I think I will make a matching worksheet–have some of the graphs/equations already printed, you have cut out equations/graphs to match. Reason being when the students (and myself!) started to fill in the blanks for the equations, it is tempting to write for the graph that is on the card, not the matching one, which led to unnecessary frustration. All the students had them matched before they left class, some had completed the filling in the blanks as well. They were really engaged and I heard some great discussions. The best thing I did was NOT print off the answer key, so I could not answer their questions with anything other than, “why do you think that?”
Which also led to this conversation in our study hall period:
S: I know I’ve made a mistake because my two ends don’t match.
Me: Oh, that’s a good catch. Did you work on trying to find your mistake?
S: No, I’m asking you.
Me: Oh, see, I don’t have the key yet, so maybe you can go through them again and see which aren’t matched up correctly.
S: I’ve already matched them but then ends don’t work.
Me: Right, so that means you must have incorrectly matched some in the middle.
S: I know. That’s why I’m asking you.
Me: Yes, but I don’t know the right order either. So did you go through them again?
S: I’ve already matched them.
Me: And we’ve decided you must have missed one. I bet if you sat down and went through them you could find your mistake.
S: BUT THAT’S WHY I’M ASKING YOU BECAUSE I’VE ALREADY MATCHED THEM.


That needed a quadruple facepalm.
Monday: I quickly went over the answers and blanks but they didn’t see anything more about it on their study guide (since the other teacher didn’t use this activity or get to discuss factored form). They did have to graph one in standard form without converting to vertex form (well, I didn’t explicitly say that so I didn’t count off if they did) and a majority did well finding the vertex and y-intercept. I also put one fill-in-the-equation-blanks-based-on-the-graph like the dominos had as a bonus. About 50% tried it (there was not a time crunch at all) and maybe about 15% got every form right. This makes me sad; I KNOW more of them could do this because they were doing it in class in front of me!! Why won’t they even try? I also feel as soon as I said (on study guide day) that these types of problems wouldn’t be on the test, they completely cleared all that information from their memory.
Tuesday: 50 point quiz. About 1/4 of the kids were out in the two of three classes (although many stayed just to take the quiz and then checked out; I even had one girl check in 8th period to take it!). The grades were at either end of spectrum–either A/B or F, although none of the Fs were horrible.
I think next year I would like to (a) use Desmos to investigate graphs and have them practice writing equations to match graphs on there. (oh, could I take a picture of a quadratic on desmos, then import the picture so they couldn’t see the equation? Then have them try to match it with their own equations?) (b) do a real-world quadratic modeling activity (basketball three-act? Mathalicious?) (c) spend more time on the dominoes activity (d) maybe start the week with the foldable and fill is as we go. But does all that turn what used to be a week lesson into two weeks and can I afford that in my lesson plans?
Other questions I have:
Why do students hate graphing as much as Dracula hates tanning beds?
Am I trying to do too much in this unit? Too little?
Should I expect them to remember more from Algebra I instead of starting from scratch?
Did I really just type over 1,500 on graphing parabolas?
Did you really just read over 1,500 words on parabolas?
What else would you like to read about on here?