Monthly Archives: February 2016

Things I Thought I Knew

Posted on by • 0 comment

Some days this job can be a bit ho-hum. Teach a lesson you’ve taught 37 times before, grade a few tests, make some copies, go home. And then some days you get to learn math that you totally thought you knew, but you had no idea. Friday was one of those days.  I’ve been teaching long enough that I probably should have known this stuff, but I didn’t. So here I am to enlighten you as well. Just be prepared for the following to occur:

Topic 1: Classification of Systems

Am I the only one that is really bad at reading directions? But then the students actually read it word for word and ask questions that I didn’t see coming because I knew what the question was really asking without having to closely read it. This week, we had a question about making an independent and inconsistent system, which I read as “inconsistent” and knew what the goal was, but then that pesky “independent” thing was brought up by students.

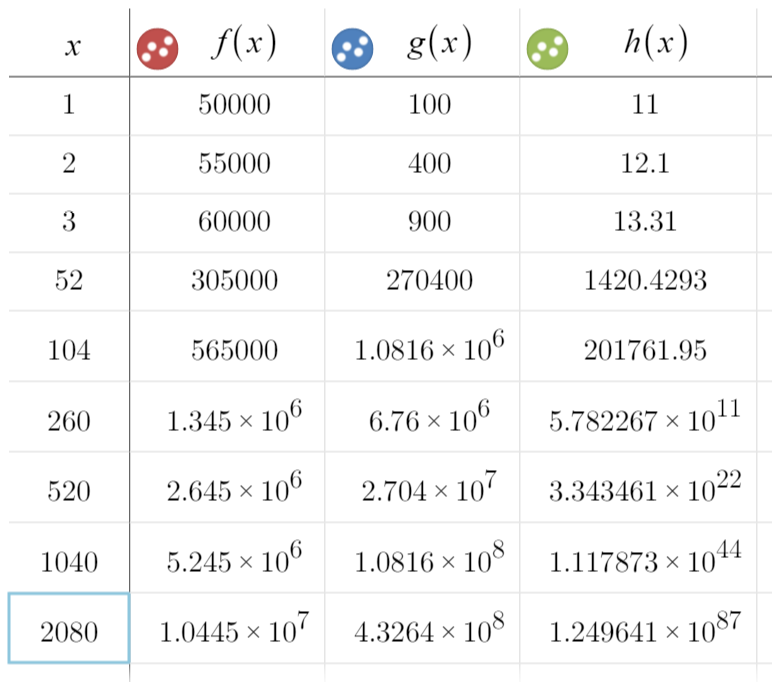
So I always thought there were three types of systems:
Independent: One Solution
Dependent: Infinite Solutions
Inconsistent:  No Solutions

TURNS OUT I was mushing two different categories together:
Category One: Is there at least one solution?
Yes: Consistent  No: Inconsistent
Category Two: Are they the same line? (Technically, “can one be formed from the other with algebraic manipulation?”)
Yes: Dependent No: Independent

So the correct categorization would be:
Independent and Consistent: One Solution
Dependent and Consistent: Infinite Solutions
Independent and Inconsistent: No Solutions

When you realize you’ve been teaching something wrong for your entire teaching career:

Topic 2: Logs grow really really slowly.

“Yes, Meg, we know that.” No, I don’t think you do. The wonderful MTBoS Search Engine led me to this GREAT activity from @Johnberray. I modified it a bit, first of all by making some pretty 1-inch graph paper:

inch graph paper

(file here) Each group got a sheet in a dry erase pocket and used their calculator to find the decimal values to graph y = log x. Then I asked them to calculate how many inches it would take for it to function to reach 2, 4, 6, and 8 inches high. (At least one group each period said 20, 40, 60, 80 so we may not have the idea of logs down pat just yet). Then I asked them to describe each distance in some way–is it the size of a pencil? classroom? from here to the front office? as tall as basketball goal?  I let them use the internet and a student showed me that if you put a measurement into Wolfram Alpha, it will give you real world comparisons! Pretty neat!

You really need to try it for yourself!  What fun we had when we started talking about how long the paper would be for a height 6, 7, and 8 inches (oh, plus go ahead and try 9!) using this draw-a-circle-on-a-map site that John had linked to. Then it turned into, how high will it be if the paper reaches the moon? The sun? Pluto? I won’t give it away, but guys, logs grow really really really really really slowly. 

Yet they still go to infinity.

One raised to any power is equal to one, oh, unless that power is infinity.

So I’m pretty good with limits. Then my Calculus teacher friend mentioned, hey, isn’t it weird that the limit of (1 + 1/r) ^ r is e, not 1?  Wait, that doesn’t make sense.  But it turns out 1^infinity is indeterminate. WHAT? But I thought 1 to any power is 1!  WHAT IS HAPPENING TO EVERYTHING I THOUGHT I KNEW?  The best answer I saw was that “we don’t know if the one is really a one”, which ok, I guess, since 1 + 1/r is never exactly one. But what if the number IS actually 1? Not like “kind sorta” close to one but ONE. If 1^infinity isn’t one, at what number does it STOP being equal to one?

I was discussing all this mind-blowing math with my friend right as class was starting, complete with dramatic re-enactments of how high the graph of log will be on Pluto and what was happening to my brain. When I came into class, a student asked what we were talking about and I said “Math!” and she said, “You really do like math a lot, don’t you?”

Yes, yes I do. 🙂

Category: Alg II, Precal | Tags: , ,

Hey, Make This Exponentially More Awesome for Me, Okay?

Posted on by • 4 comments

Monday I spent a couple hours falling into the #MTBoS trap of lesson planning: having so many shiny pretty ideas that I can’t decide what to do! I was trying to figure out how I wanted to start my exponential unit for PreAP Precal. Yes, they’ve seen it before, but I didn’t think they had a concept of EXPONENTIAL BEATS EVERYTHING (I know I really didn’t until my [REDACTED] year of teaching math.)  So this is what I came up with:

You just started a new job. Pick the best salary option and be prepared to support your opinion:
Option 1: $50,000 a week, increased by $5000 each week.
Option 2: $100 times the square of the number of weeks you have been working (I didn’t really know a better way to describe this?)
Option 3: Start at $10 a week, increase by 10% each week.

It was a weird day yesterday with some classes half-full due to class meetings, plus I had some tests to go over, so we only had about 25 minutes to work on it. I let them have 10-15 minute to discuss in their groups. Many people started with a table, which is quite deceiving at the start. A few groups finally asked, “how long are you working there?” To which I replied, “That’s a good question, how long are you working there?”

Most decided to focus on one year, and thus chose option 1. A few ventured out further and chose option 2. (Maybe next year I’ll make so option 2 overtakes option 1 just before year one instead of just after?) Most could not figure out an equation for option 3 (which didn’t bother me, especially when they haven’t seen exponentials in over a year), so just crossed that one out immediately based on the first few weeks.

After each group gave their reasoning, we worked out a table on the board, starting with 1, 2, 3, 4, 5 weeks, then figuring out the equation for each week. I then gave each group a time frame-1, 2, 3, 5, 10, or 20 years and had them figure out the weekly salary for each option.  The bell rang right in the middle of posting the results, but we still had fun talking about making $10^22!

Today I showed them the graphs in desmos and we talked a bit about them:

(Desmos file here) But I think we FINALLY got the power of the exponential when we put it in table form:

exp 1

I mean, look at how slow both the linear and quadratic are growing. 10^8 after 40 years? That’s not even worth getting up in the morning for! I also wrote out the final numbers on the board while they were working on the next task, using all 87 zeros.

Yup, I think they will say that exponential will win every time now. 🙂

As we were working on it, I thought of a lot more things we could extend with:

  • Figuring out the time to switch by solving a quadratic (option 1 & 2) or by using technology–either Desmos or using Excel?
  • Have them write an actual recommendation of which salary to chose and why.
  • For the first couple of years, students were wondering if making so much at the beginning would make you have more money at the end of the year with the linear. What a perfect way to bring in area under the curve! Especially because they could actually calculate the linear function’s area with just one trapezoid, then I was thinking just to use the integral function on the TI for the other two.
  • Of course it could also be a nice lead-in to logs: when will each salary hit $100,000? $1,000,000? $10,000,000?  (Also nice to look at graphically!)

So this post is serving as my reminder to myself to devote some days to this next year, and try to do some of these extensions. But if any of y’all want to try it out and make it awesome as you are wont to do, please do and report back! I’ll be chillin’ with my cool $10^87.

Category: Alg II, Precal | Tags: , ,