(See more Alg II files and FAQs here)
So this was an interesting chapter…one that I think I improved from last year, but could still have used more connections and also some more activities (e.g. double stuf oreos wafers and creme).
It started with a great discussion:

(hey guys, hold out for a couple more chapters when I got a new phone that does pictures a whole lot better! Sorry for the random quality until then.)
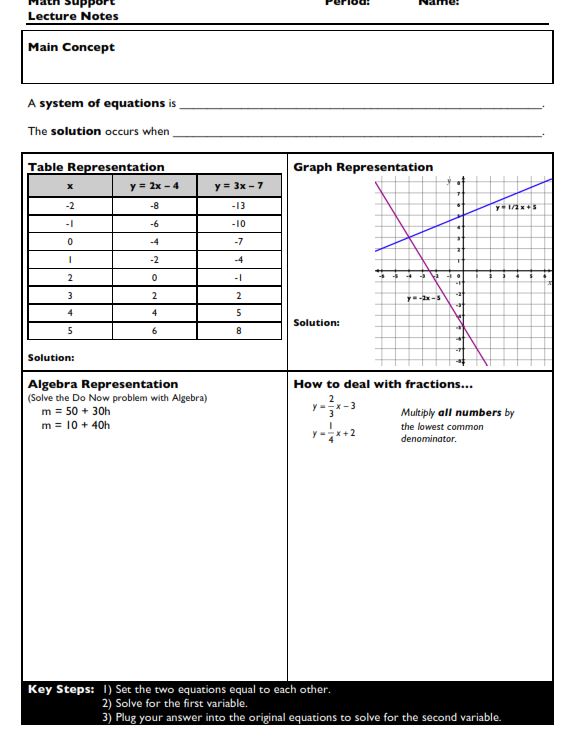
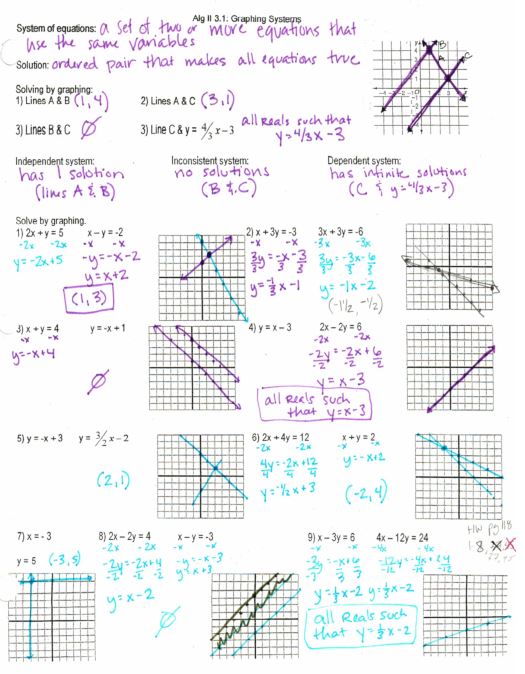
(file) So, guess what? I had been teaching the types of systems wrong for a long, long time! To recap from that post, the correct way is:
Category One: Is there at least one solution?
Yes: Consistent No: Inconsistent
Category Two: Are they the same line? (Technically, “can one be formed from the other with algebraic manipulation?”)
Yes: Dependent No: Independent
So the correct categorization would be:
Independent and Consistent: One Solution
Dependent and Consistent: Infinite Solutions
Independent and Inconsistent: No Solutions
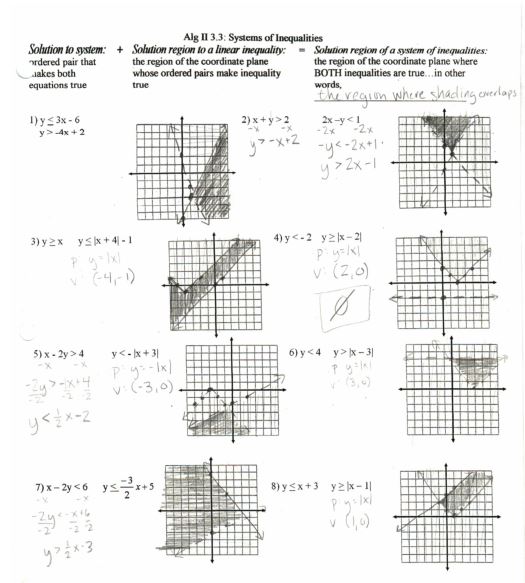
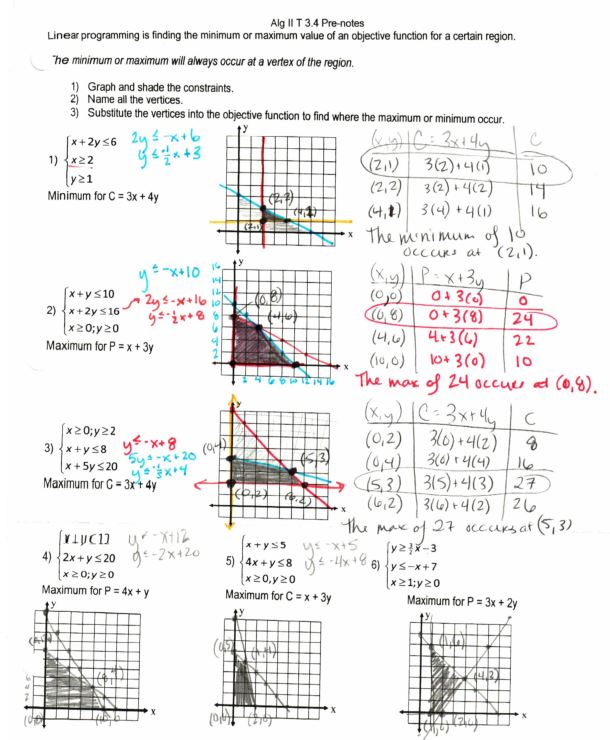
Then we did some substitution, some new stuff here: being really conscientious on boxing equal things and also looky there in #6, doing substitution with quadratics!


(file with these questions and more practice)
and I even went a little crazy and did this:

(This may also be why so many of my students remembered how to expand (x – #)^2–we did them a lot of them throughout the year!)
Elimination.

I was pretty proud of the practice I prepared for the pupils:

(file) The last set was interesting when they didn’t choose the method I thought they would!
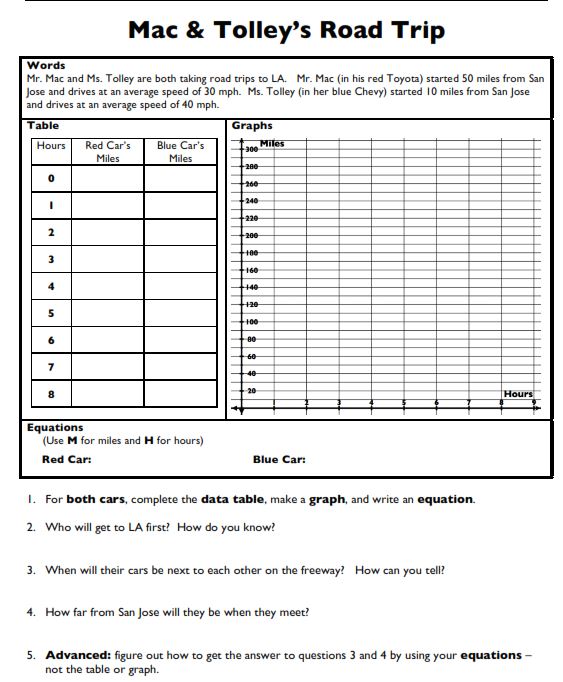
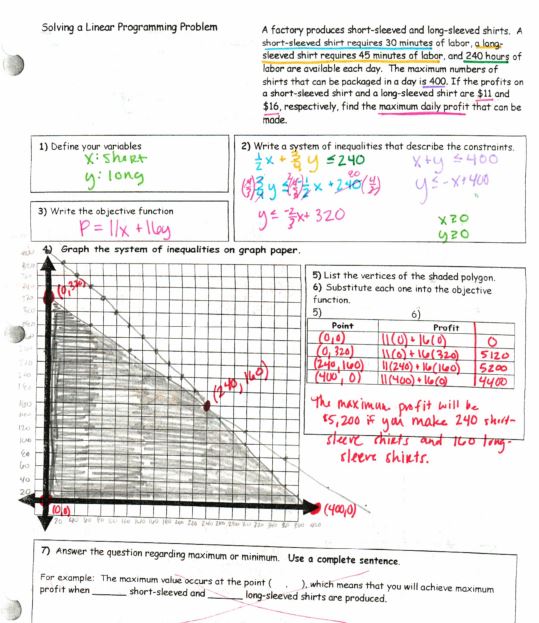
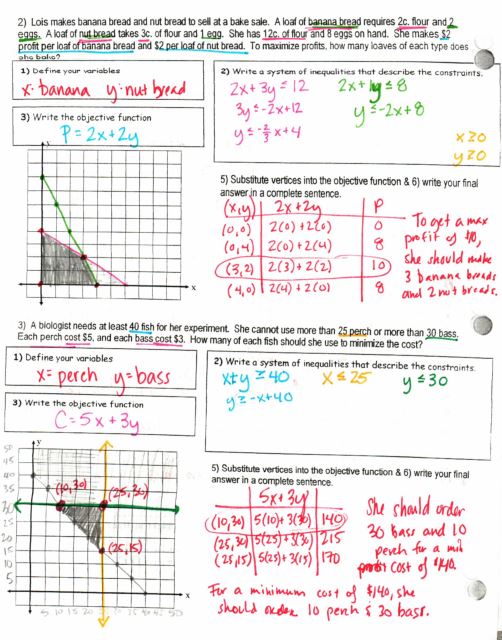
Did I hear someone say they’d like to see more textbook-like systems of equations word problems? Here you go!


(File with these & more practice problems) But I was able to add a pretty cool activity from Amy (@sqrt_1) where the students made their own word problems. The only thing I changed was condensing all the work onto one page for easier grading:


(instructions and worksheet) It was a nice day and a lot of the students had fun with it (how often do they get to break out the colored pencils and color? I also gave bonus points for the most creative one from each class and put my favorite one on the test!). I will say next time I will have them show their work that they tried it! (I said they had to do it on their notes, but not turn it in.)
Have I told you how much I like doing group speed dating?

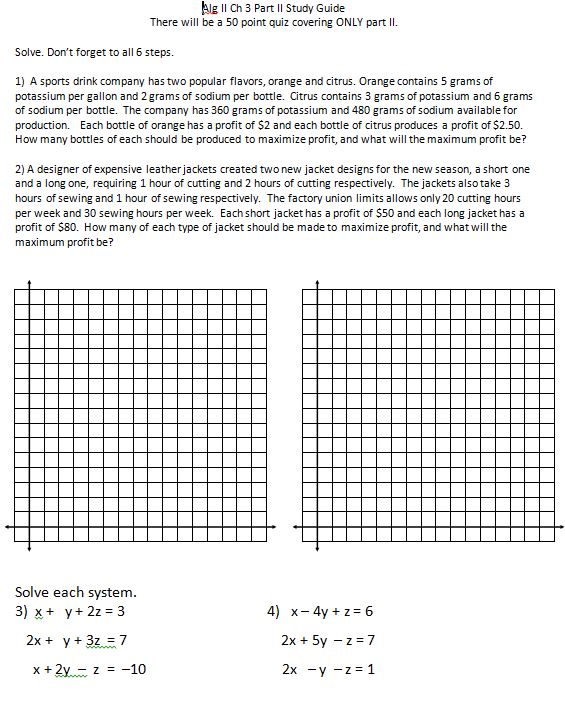
(file) Then it was study guide time!
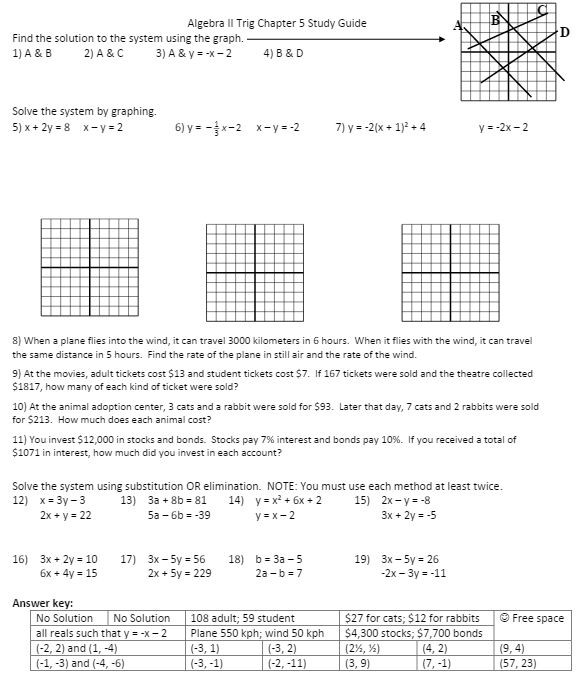
(file and video key part I and part II) As I said, a lot of room for extensions, activities, and connections in this chapter that I just didn’t have the time to incorporate. TBH, if it’s the night before the lesson, go ahead and use some of my stuff, but if you have time to plan, please go see all the more awesome things there are out there in MTBoSland!