tl;dr: Files for unit circle, graphing trig, and inverse trig functions.
So I’m going to post my precal files in the order that I taught them (see more of my precal files and FAQs here). I met with a PreAP curriculum committee at the beginning of last school year, and they suggested that we do all the trig stuff in the fall, then go all the way from functions -> quads -> polys -> exponentials -> rational -> limits -> derivatives in the spring. It did work really well in the spring, but I need to do better at spiraling back to trig–I have a fear they won’t know what sin of pi is next August!
Ok, are you ready? Here we go!
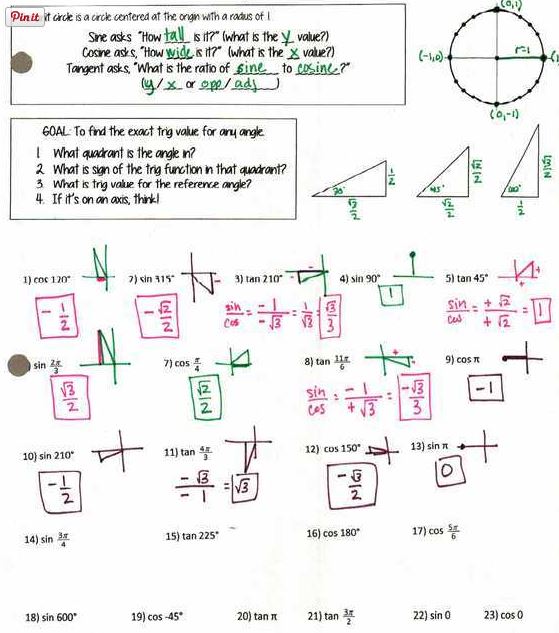
Starting with trig values at a point:
File here.
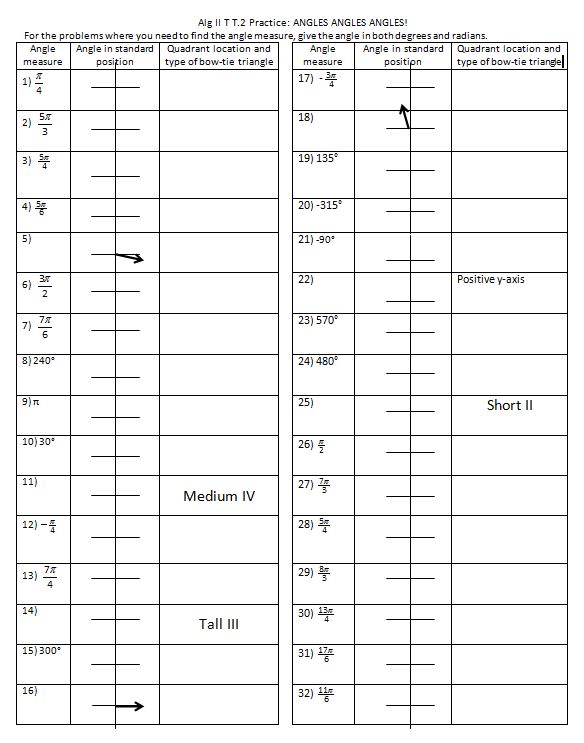
Then angles review, but I think I like the worksheet from Algebra II better.
File here.
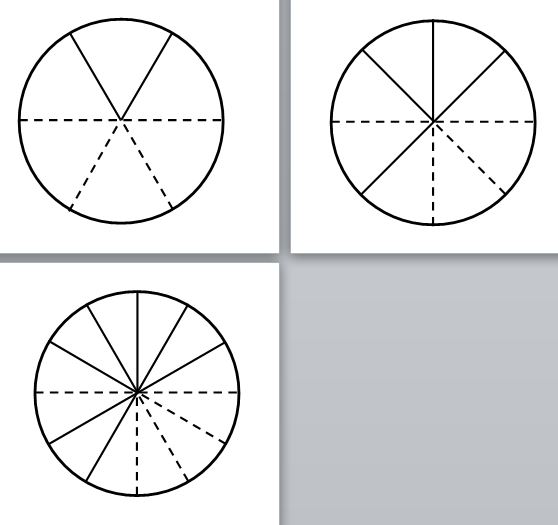
Then the unit circle review:
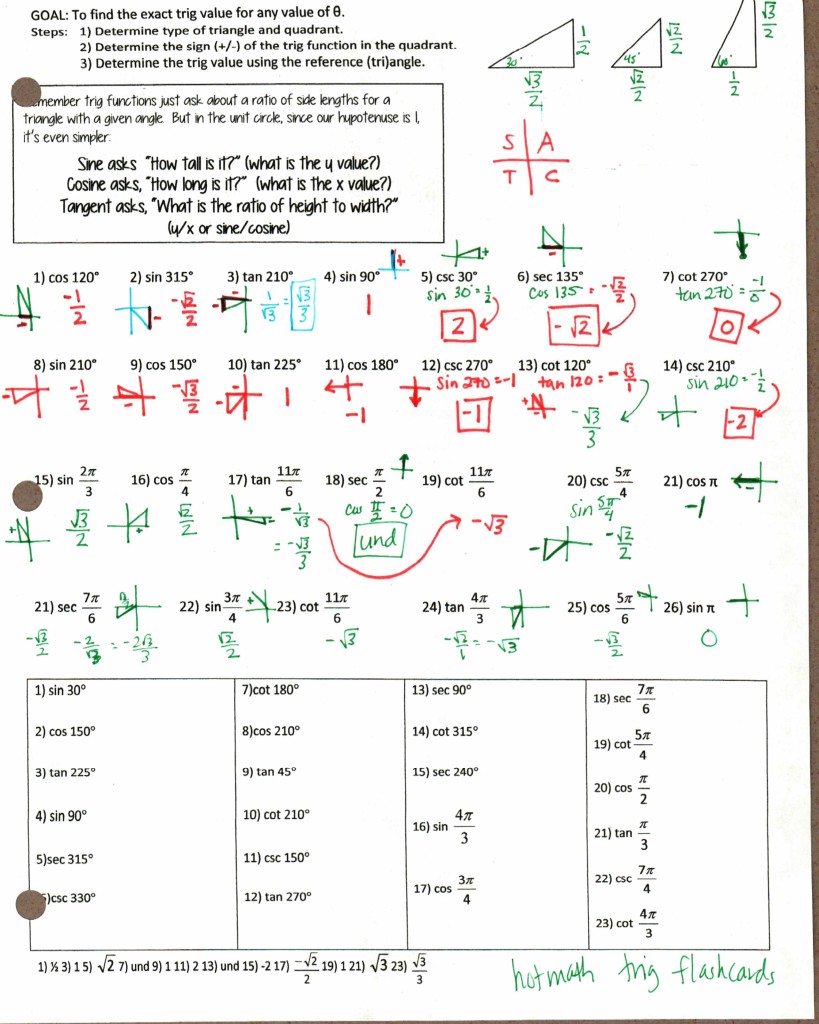
File here. We also talk about the hand trick. The hotmath at the bottom is for one of the better trig value flashcards website I’ve found.
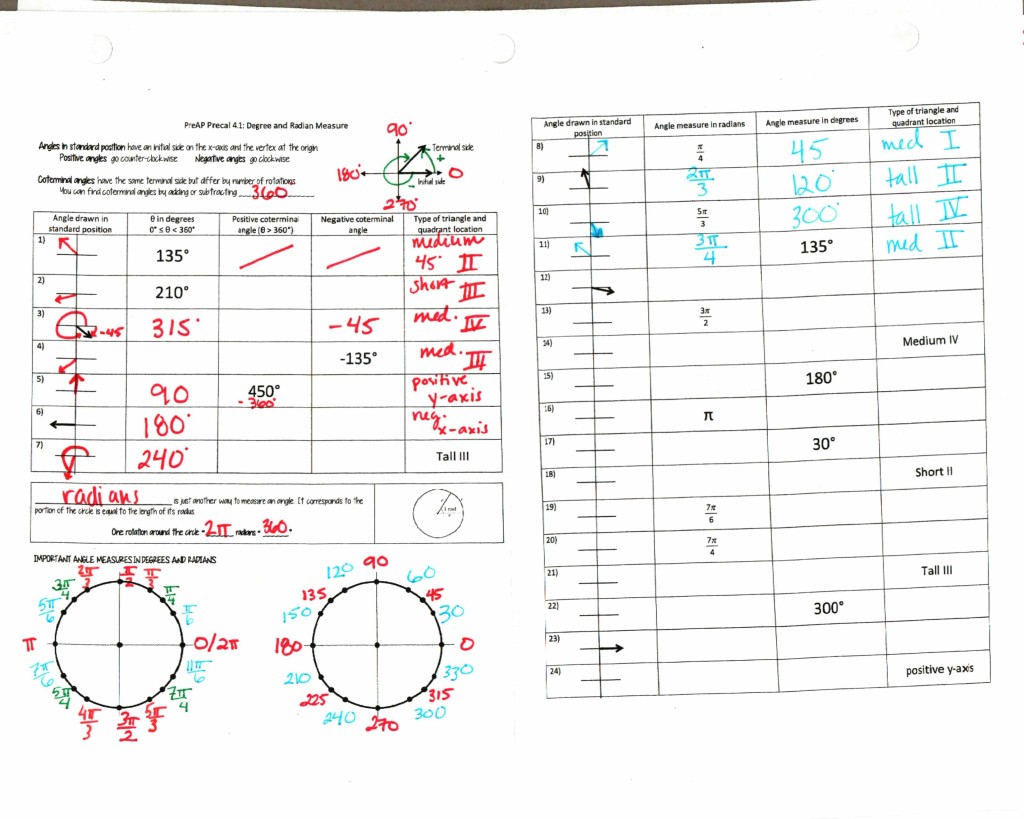
The next day we expand past 0 and 360:
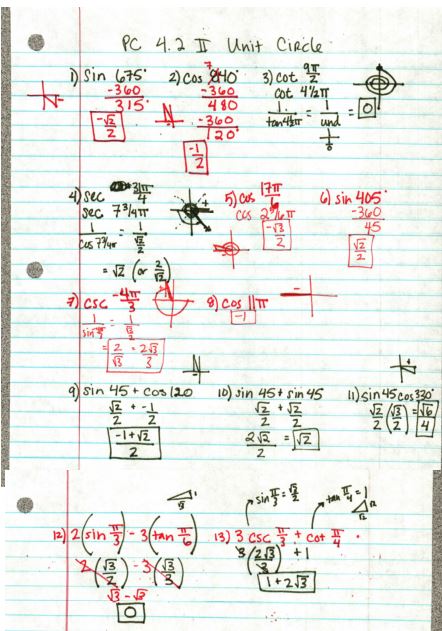I use a worksheet from an Algebra II/Precal joke book for homework (which I just learned is frowned upon? I must say that these are usually well done and have some good questions that catch conceptual errors).
Then it’s time for one of my favorite group work worksheets, (that I already wrote about here):
File here.
At this point we stopped, reviewed, and took a small quiz.
File here.
Then it’s onto graphing. This is about the time I first learned about the windowpane method, so I taught some classes one way, some the other, and some both. This shows the window pane.
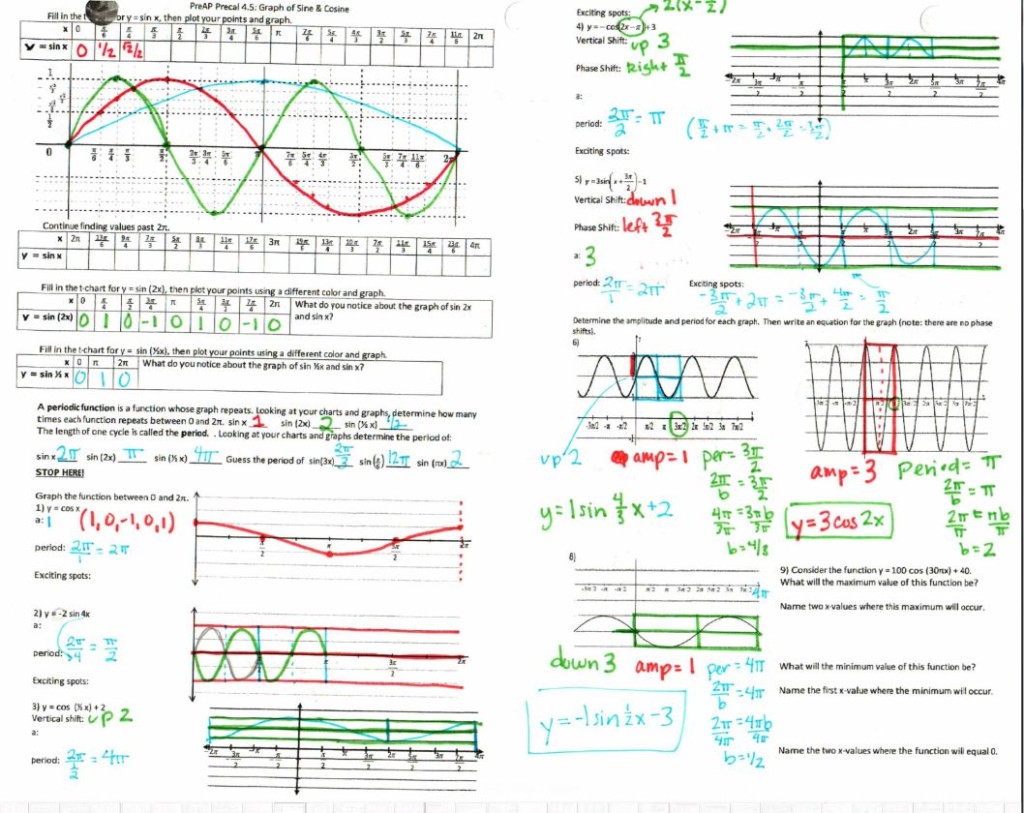
File here. This should have gone faster, but took over a day. The graphing from scratch at the top was like pulling teeth.
This is their practice/hw, which shows the old way of marking the graph into “exciting points”
File here.
Then we did a real life sine problem from Math Teacher Mambo.
Here’s her post on it. Be prepared: it looks like a cosine graph so they all wrote cosine equations because who reads directions? Then I had to tell them to actually read #7. Next year, I may have them choose whichever function they want, then make the last question be “convert from sin to cos or cos to sin.”
Next, cosecant and secant:
File here. I teach cosecant and secant graphs using a suggestion from a student: we sing “The Grand Old Duke of York,” since when you’re up, you’re up, when you’re down, you’re down, and when you’re only halfway up, you’re neither up nor down (asymptote!).
Ugh, tangent graphs.
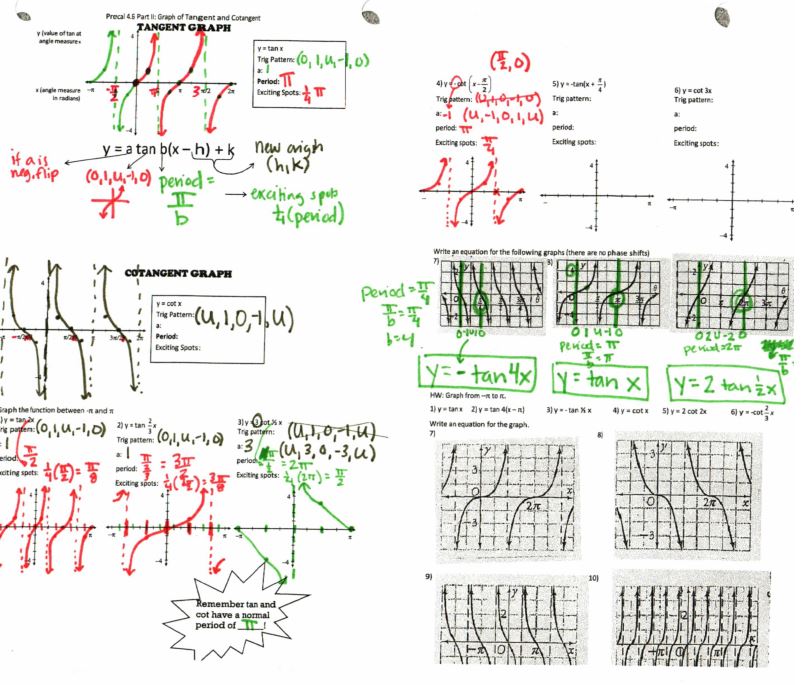File here. This is another example of the “exciting point/pattern” method of graphing, which looking back, I think I like better. Or maybe I need to come up with some hybrid.
Then, because it ties in so well with graphing, we did inverse trig functions in this unit.
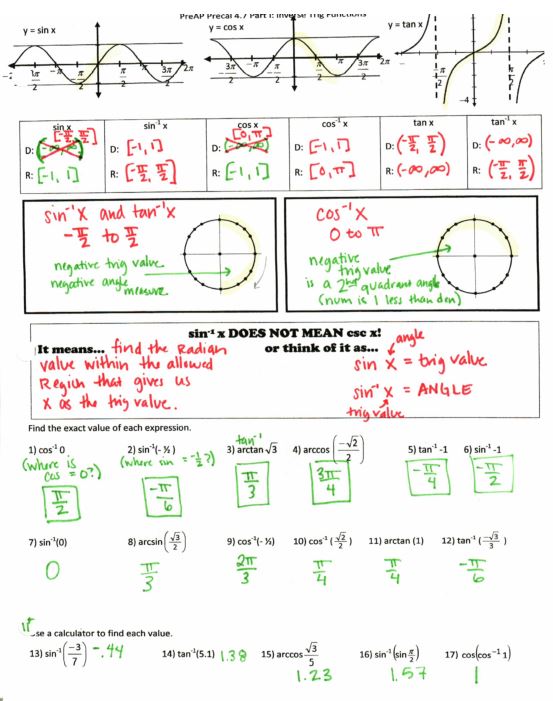File here
File here. Even if you’re not a homework gal or guy, you may still want to use those last 3 problems as a lead-in for the next section
File here. Although next year I want to spend more time on the even/odd/unit circle-ness of sin/cos to discuss, “ok, well, we can’t use 4p/3 in the allowable region for cosine, but what angle in the allowed region should have the same cosine value?”
File here. *Note! The answer to #17 should be pi/3, not 2pi/3! It should be fixed in the file. Thanks to Chikae for spotting that!
Study guide time!
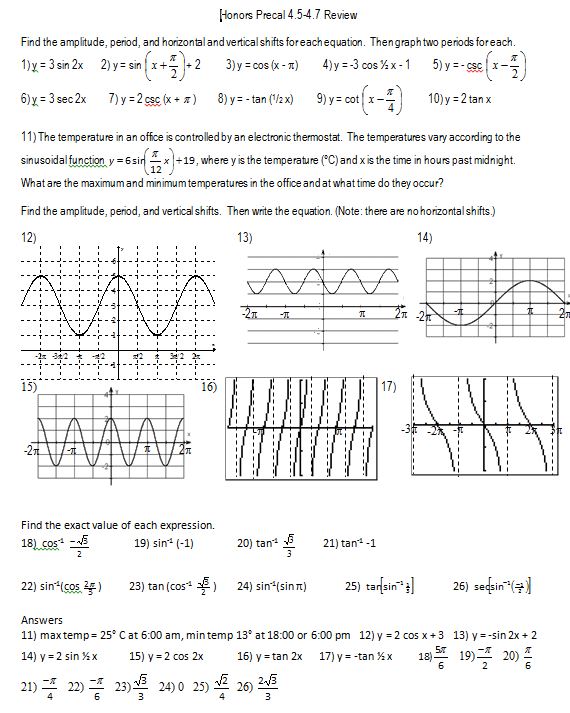File here. And, yes, it comes complete with review powerpoints (that could also be used for whiteboard practice). And they come in both exciting points and windowpane varieties–choose one or both!
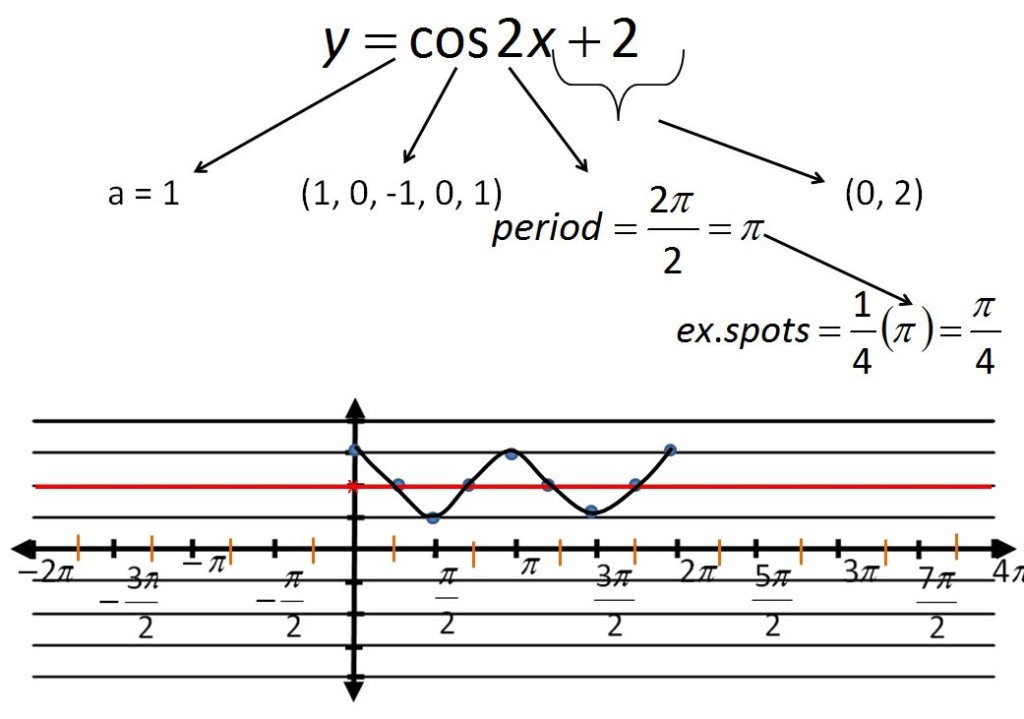
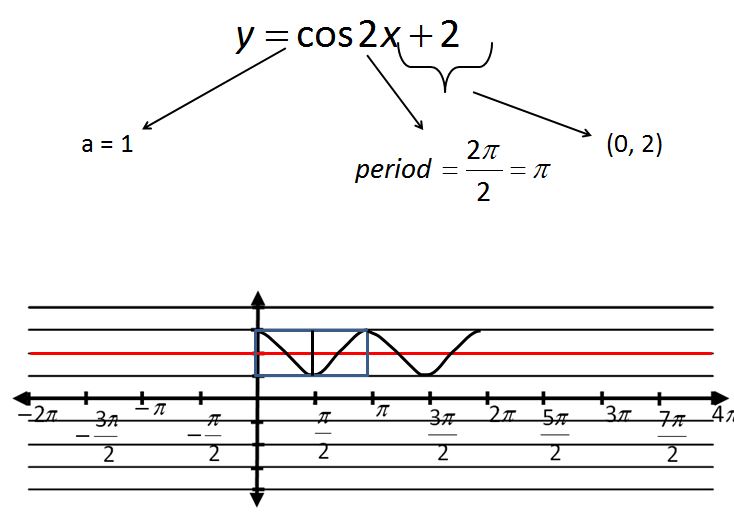Exciting Points file here. Windowpane graphing file here.
But wait there’s more! If you act in the next 20 minutes (just like the real commercials, the 20 minutes starts whenever you read this 🙂 ), you can get a video of me working out some of the study guide problems!
#11-17 video here and #18-26 here.
I post these the night before the test and the students who watch them are very appreciative.
So, be honest: am I the only one who could Trig all day? (Except for tangent graphs, obvs!)
.doc file
