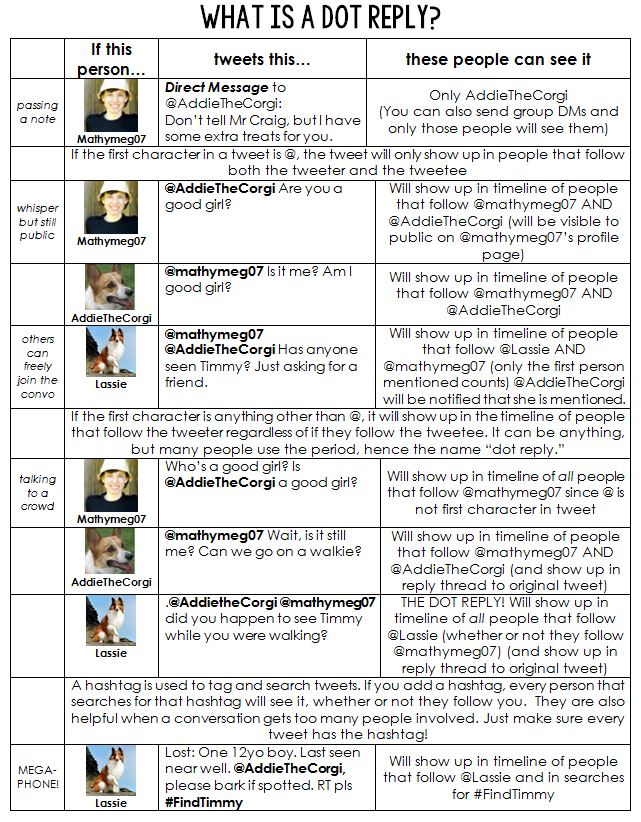
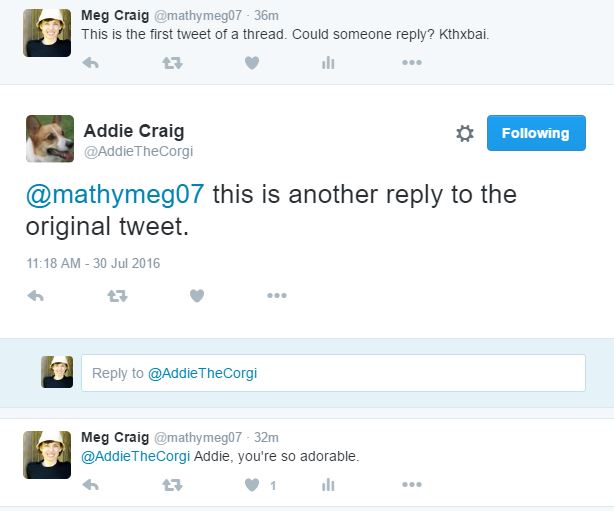
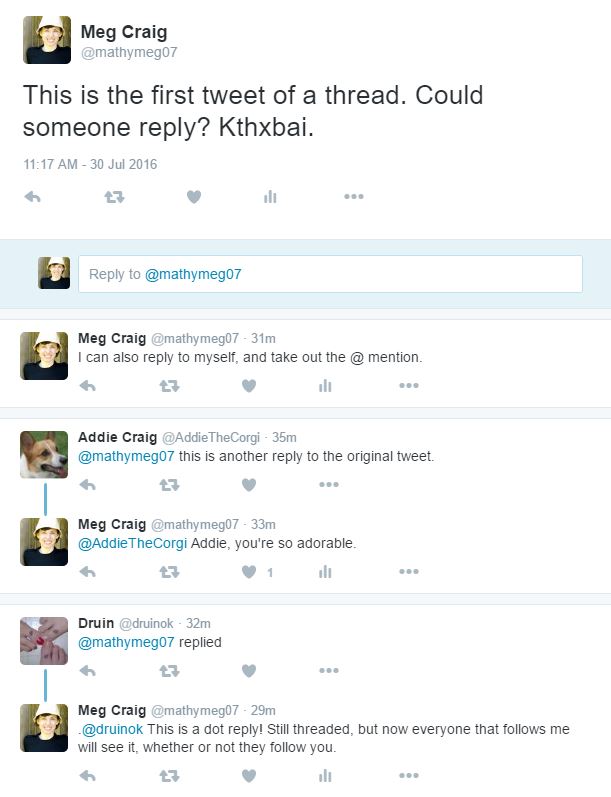
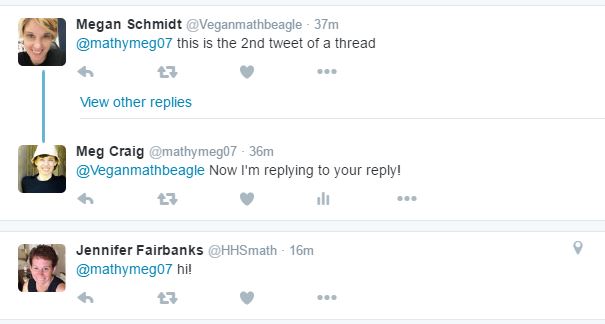
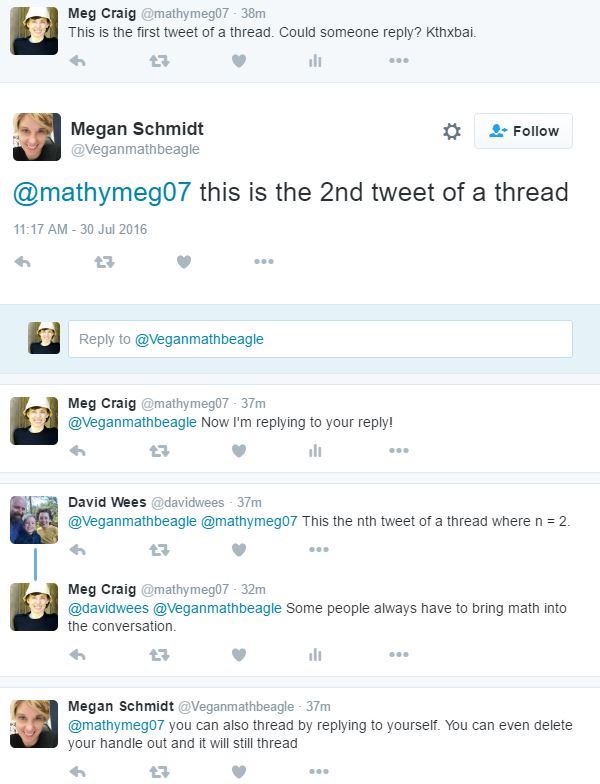
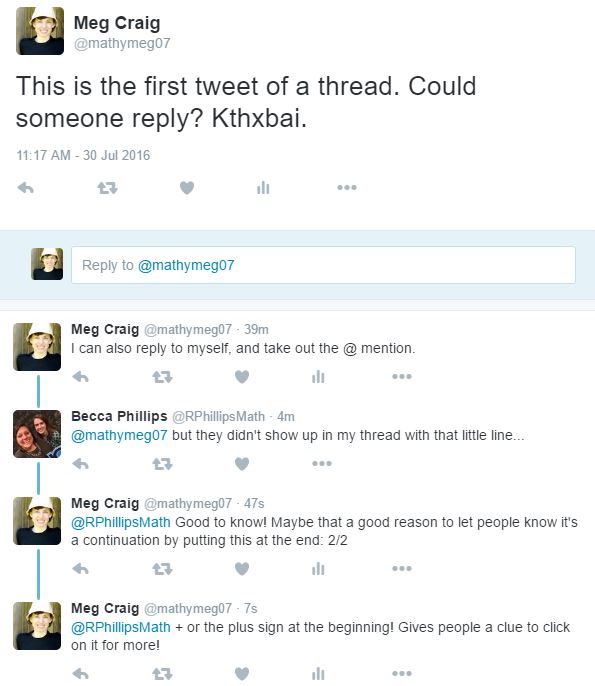
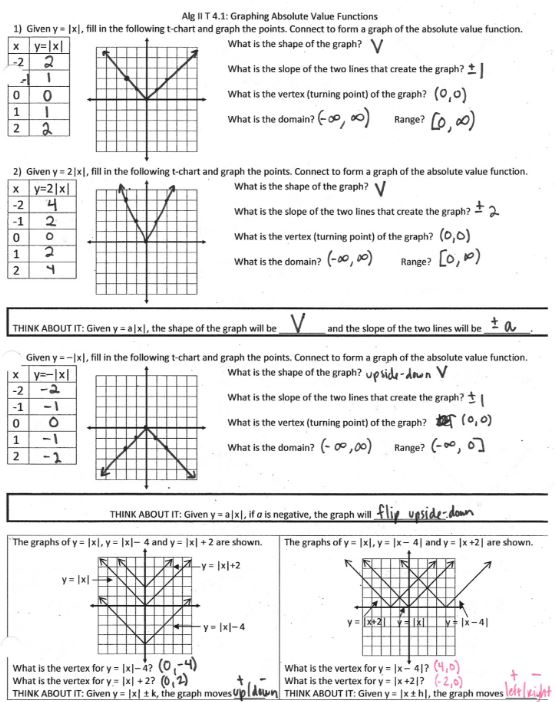
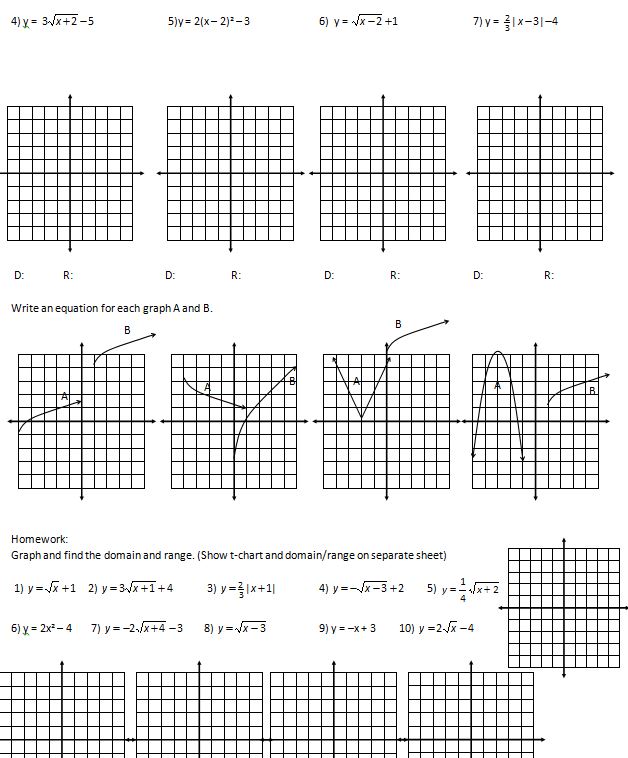
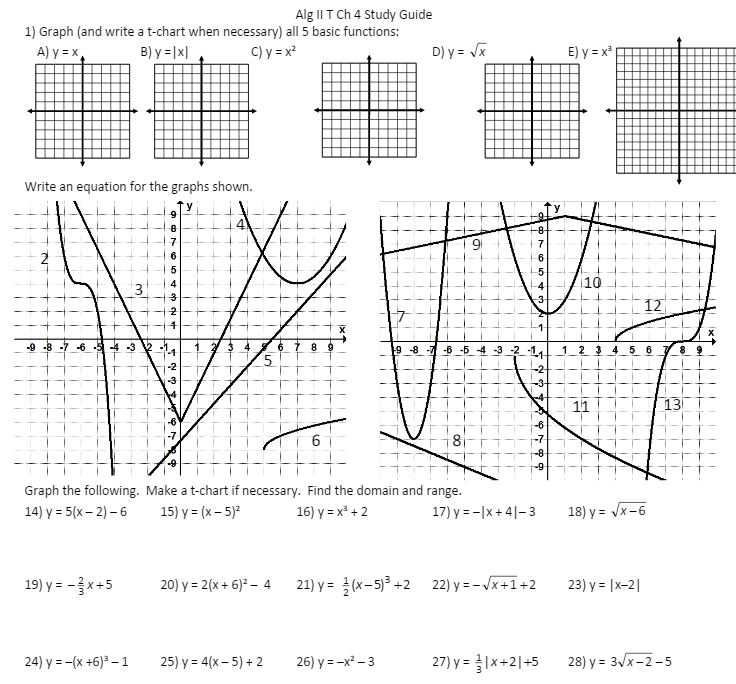
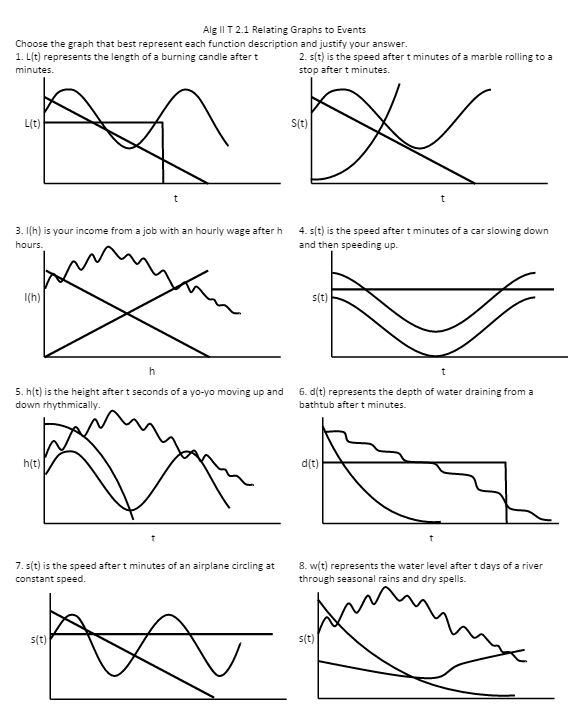
Maybe it’s just me: I star A LOT of stuff in my blog reader and I star (ok, “heart” now) a lot of tweets, but then never go back to them! So I thought I’d try to post weekly things I’ve starred so (a) you can enjoy (b) I can remember and (c) the posters can get a shoutout. 🙂
PSA: You don’t have to make a fancy post to let someone know you’ve appreciated something they’ve done. A tweet, retweet, or blog comment can really mean a lot to #MTBoS newbies members! I’m going to try to keep these posting going weekly, as well as tweeting someone when I use their stuff! 🙂
My starred posts this week:
Not a post, but if you’re in the Southern US (we’re going ahead and defining that as “Tennessee-adjacent”), be sure to add your name & info to the roster! Hope to plan a mid-fall tweet up!
This first post from Hannah (@girl_got_range) is a great long form about vulnerability in teaching and in life.
Go ahead and read all of @Anniekperkins‘s first 5 posts, but be sure not to miss the latest one about how her “uncompromised beliefs” ended up being a bit, well, compromised.
For something a bit more lighthearted, check out Casey’s (@cmmteach) ABCs of TMC.
Getting a chance to hang out with Brian (@_b_p) at TMC reminded me yet again of his quiet succinct genius. Be sure to follow his blog for little nuggets of awesomeness, like this great way to introduce end behavior. I can see many ways to use this same setup, such as limit notation and his example of sigma notation.
Sarah (@mathequalslove) collected some great resources from 3 different blogs-I love the last one about asking what question each expression answers. And I love the cubic meter. And I love the crime scene. Ok, I guess I love all three!
Also check out her broken circles first day activity. And while you’re at it, Amy’s (@zimmerdiamonds) first day ice-breaker with a secret agenda (watch the periscope video here). And then check out Beth’s (@algebrasfriend) entire collection of first day activities. Basically I need a month of first days.
If you’re looking for a one-stop shop for expert advice for a newbie or oldie, be sure to check out Elissa’s (@misscalcul8) new How To posts. She’s already made them for teacher moves, questioning, and building relationships (I also predict an organizational one soon). Even if you’ve heard some of the stuff before, I bet you haven’t heard all of it before!
Because Julie (@jreulbach) likes to mock me, she is going all gung-ho on Algebra II the first year in over a decade that I haven’t taught it! Be sure to join her blogroll and submit posts to her recaps! Also check out her post on reliving TMC16 through video!
In those TMC videos, I would recommend Joel’s (@joelbezaire) Math Game with the Lame Name and Gregory’s (@mathtans) genius cubic formula parody song (I’m still amazed how he was able to write that!!)
And now some of my starred tweets:
#mathart A family of circles, whose radius is the distance from the top of a circle, that from a cardioid. pic.twitter.com/E3cxIaD3fC
— Luke Walsh (@LukeSelfwalker) July 30, 2016
No classroom window you say? No problem I say! I think I love it! pic.twitter.com/KFtLq2hGFf
— Melynee Naegele (@MNmMath) July 30, 2016
@druinok @mathymeg07 @_b_p Statistically, I am better than following 1000 people. In many other ways, I am better than all humans.
— MTBoS Blogbot (@MTBoS_Blogbot) July 30, 2016
This is pretty cool. #1 New Release in Math Teaching Materials! https://t.co/ddO9IGjWhj #tlap #satchat #leadupchat pic.twitter.com/WaSdUwqHF4
— Denis Sheeran (@MathDenisNJ) July 30, 2016
Important infographic for those lacking mad dance skillz. You’ll impress EVERYONE w these moves. By @IsabellaRotman pic.twitter.com/FoNM9wsq5N
— Janet Ng (@janetngbio) July 28, 2016
@mrdardy Nspire? 84? We use Nspire & I’ve steered away from step-by-step but do have “Can you find” for geom day1. pic.twitter.com/lYbrw5ptZx
— Jennifer Wilson (@jwilson828) July 26, 2016
@misscalcul8 Try the incredible shrinking notecard. https://t.co/NbbHoIlHMQ
— Kathryn Belmonte (@iisanumber) July 24, 2016
And as a reward for making it through, let’s end this first post with a song!
The #TMC16 Party Anthem, two camera angles with visible slides https://t.co/QE1mvwnnAS
— Jonathan (@rawrdimus) July 23, 2016