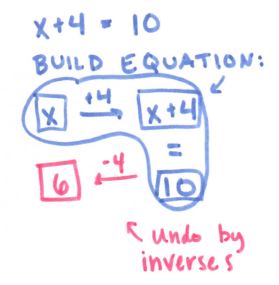
Astute readers of my blog may remember my ramblings of the “flowchart method” last summer (and my use of it at the start of the year in Algebra II). After not focusing on it for quite a while, I brought it back for solving logs and exponentials, and it helped so much, all the way from struggling Algebra II students to PreAP Precal rock stars. Next year I really want to focus more on carrying it through all that we do, but baby steps first.
My introduction to composition of functions remained the same, next year I want them to really focus on writing the steps of each function in order. I changed up how I introduced inverse functions, but I’m not sure if it went better than the previous year or not. I need to work on melding the two together (I also think a couple more days for this unit would have been reallllly helpful, but Spring Break!).
I started by having them do the first row on the NTM below as a bellringer. Whoa, that’s weird, 3 and 4 have the same answer! And it’s what we started with! Then we did the next row, whoa, so 7 & 8 have an output of x! That means anything we put into it will come out the same!
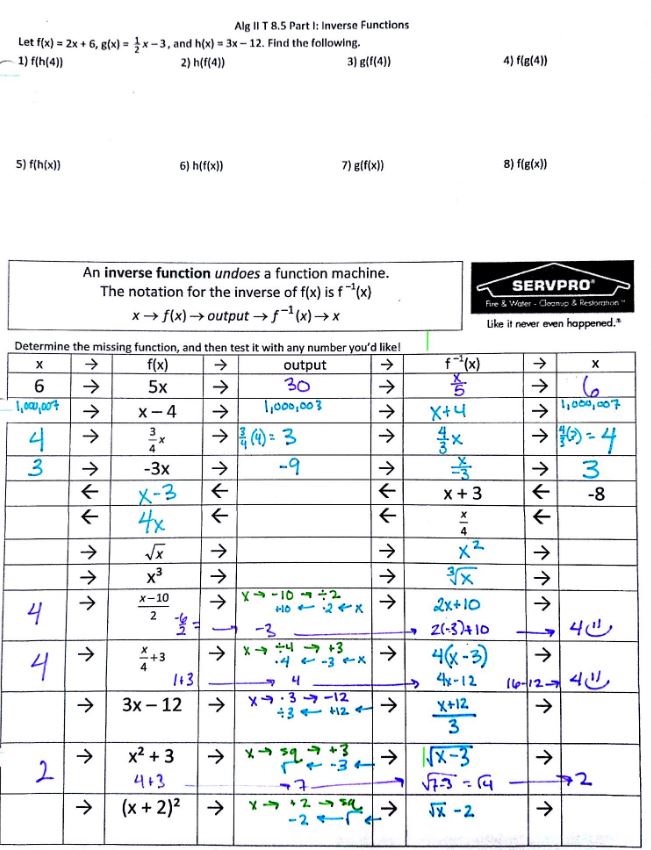
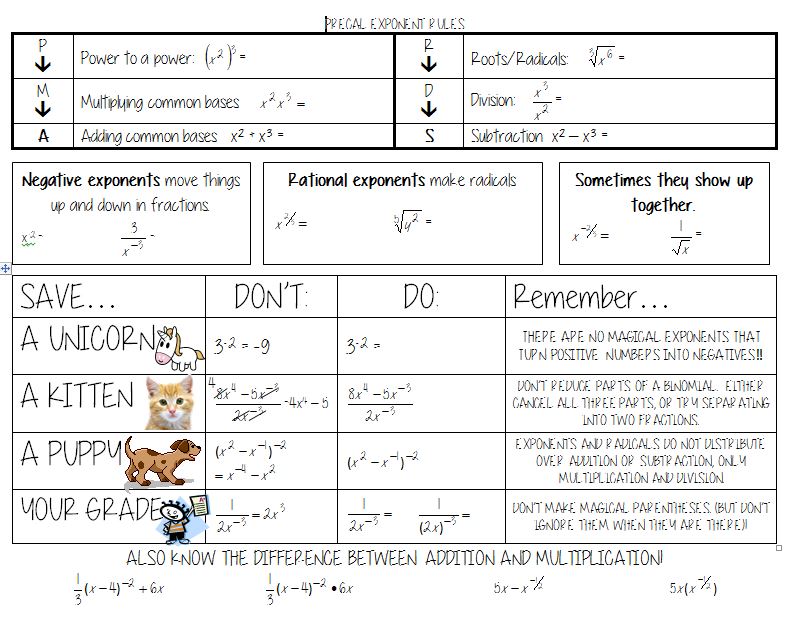
(file here) (If you’re like my students, you may not get the ServPro reference: they are a disaster cleanup company with the tagline “Like it never even happened,” which became our tagline for inverse functions.) After explaining the joke, we worked on the chart, determining inverse functions and checking with whatever number they desired (We don’t make a big deal about 1:1 functions until Precal, although we did talk it about the next day a wee bit). And this is where building up the function machine the day before would have been super handy! Let’s just reverse the machine! (I also wanted to do Bob’s Inverse Function Partner Activity, but again, time!) Then the next day I felt I had to discuss some more properties of inverse functions, but again, not the greatest:

(file here) Trying to do too much at once, so we didn’t get to focus on the chart at the bottom: “Oh, so we’re really using inverse function machines when we solve equations!”
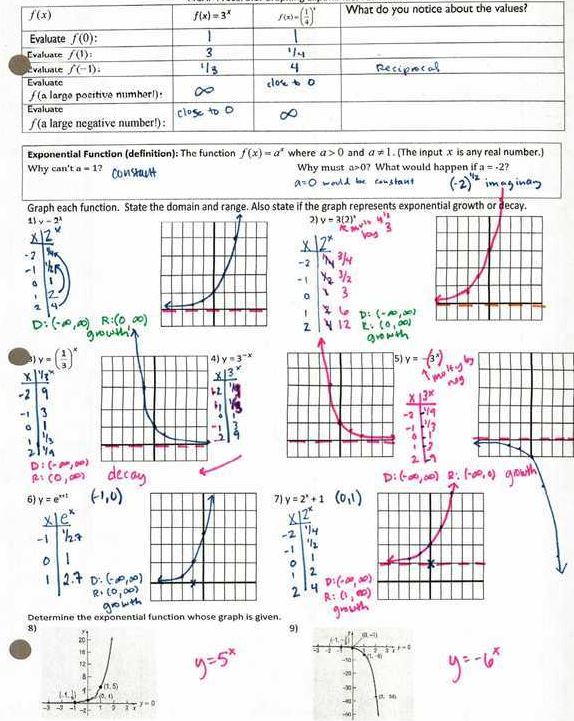
Then the next day we did exponential equations:

(file here) I really wanted to do the Zombies! Activity but, again, time! So at the end of the day we did #14 with our calculator, leaving the last two for homework. So much frustration! “Really, there’s no other way to solve these?”
Well, maybe there is….
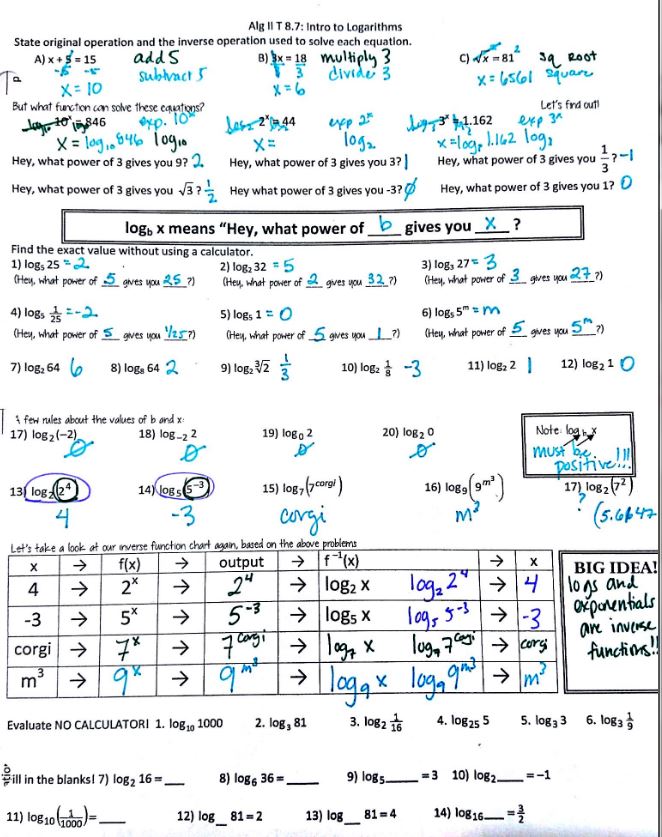
(file here) Thanks to Kate for the fill-in-the-blank problems at the bottom. I would probably save the beginning part for the next day, when we are actually solving equations. But look at that glorious chart! Oh, so you’re telling me that logs and exponentials are inverses?

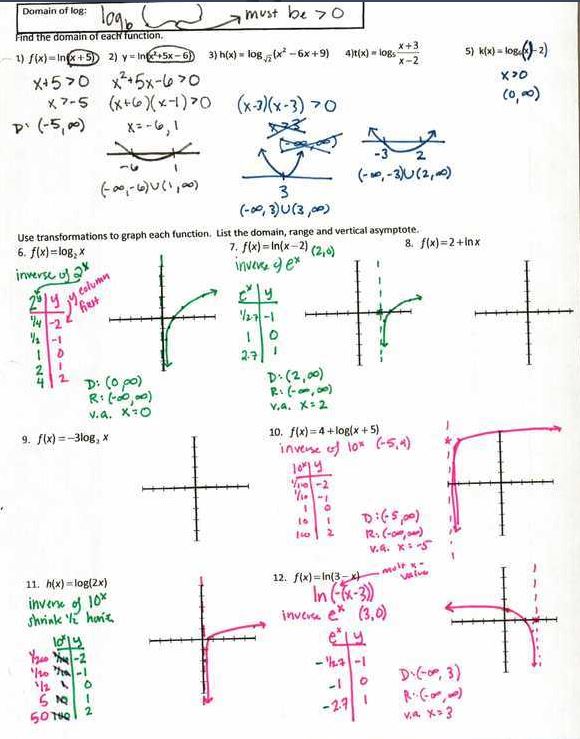
The next day is when we REALLY focused on the inverses idea:

(file here) I wish I would have had them write down the actual flowchart on these, though, just to reinforce the fact that log base 6 in the inverse of 6^x. As in, the number matters! You wouldn’t undo +3 by -4! So you wouldn’t undo 7^x by taking just log!
I also always have this conflict with myself, as illustrated here:
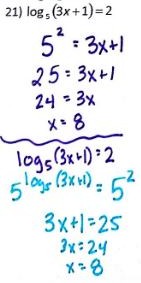
Teach “undoing a log” by converting to an exponential equation or as exponentiating both sides? I usually stick with option 1 in Alg II, then bring in option 2 in Precal. But maybe with the flowchart option 2 would make more sense?
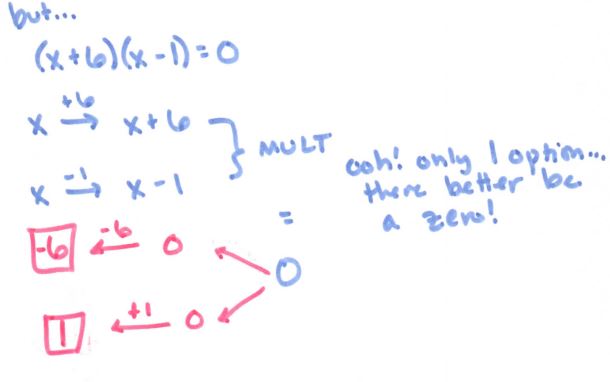
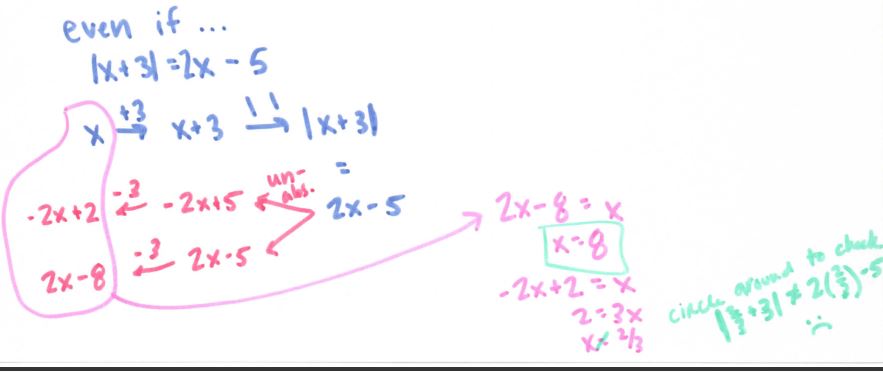
Anyway, speaking of the flowchart, here is where it gets super useful:

(file here) Look how beautiful that is. No one thought to make #12 into 5 ln x! And it really focuses on ln and e being inverses of each other. We held off on the homework until we had some group whiteboard practice the following day, using slides like these:


(file here) Now, don’t get me wrong, we still struggled. We spent two days on the study guide (file here, with video key part I and part II) after this and I still had students try to undo a log by using a log. However, I also saw a lot of students that have been struggling do really well on this test–because they had a strategy they could use to attack each problem. (We also talked about how hard it is to intuitively feel like your answers is correct, so let’s use the calculator to plug it back in–this was complete news to many of them that they could have been doing that for any equation we solve!) And it wasn’t just the struggling students who were fans–I overheard one top-notch student say to another, “Hey, did you write the flowchart? It really helps!”
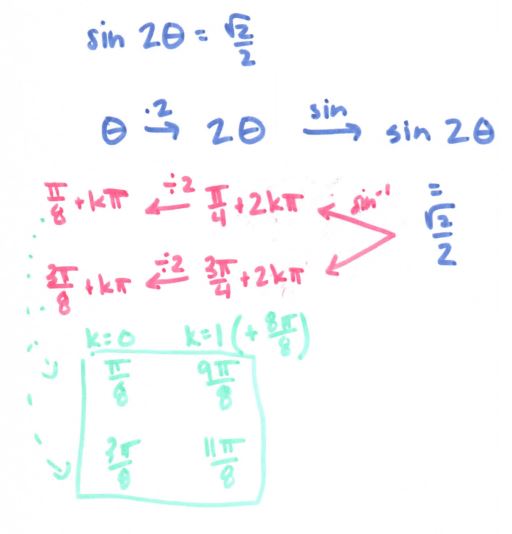
As I mentioned, I also used it in Precal with great success:

(File here) We also used it for actually solving equations, but I can’t seem to find that file! Doh! But hopefully you get the idea: flowchart it!





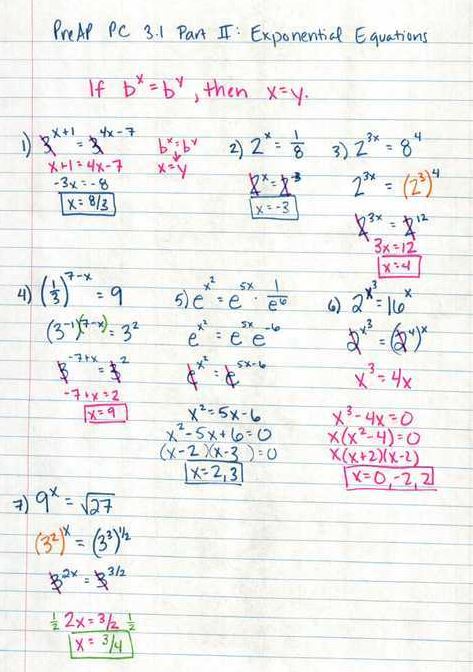




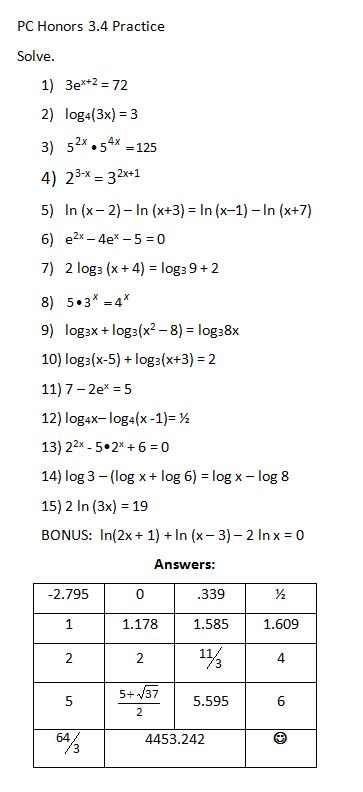








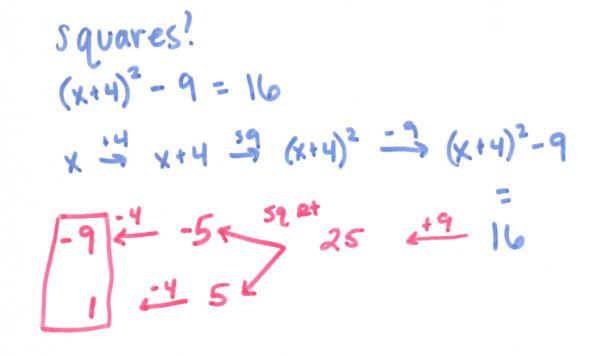

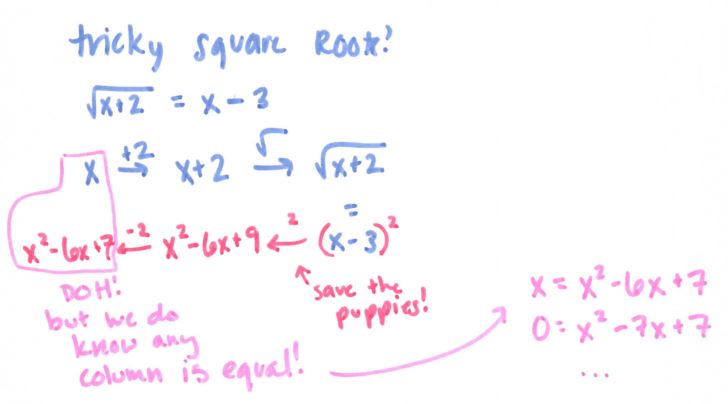

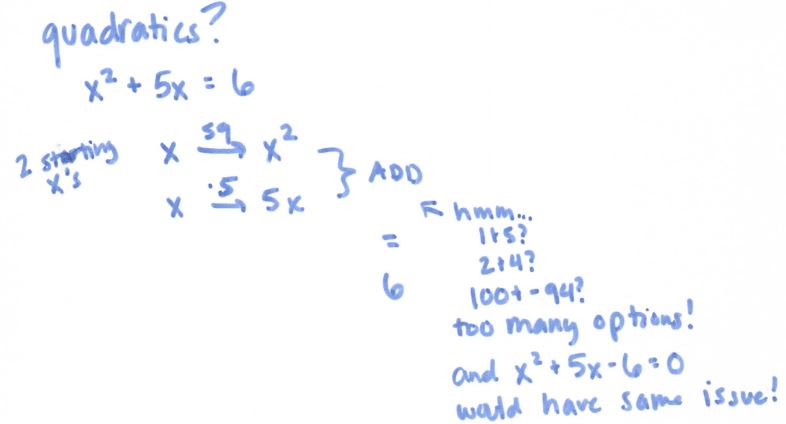
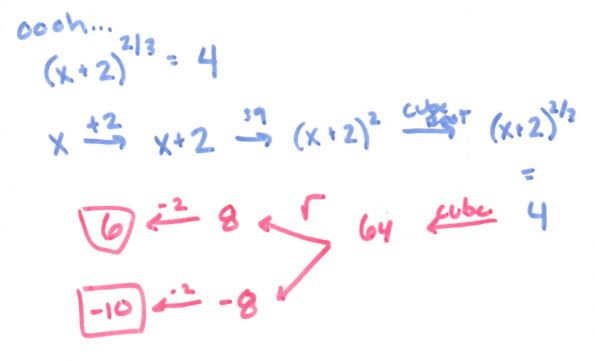


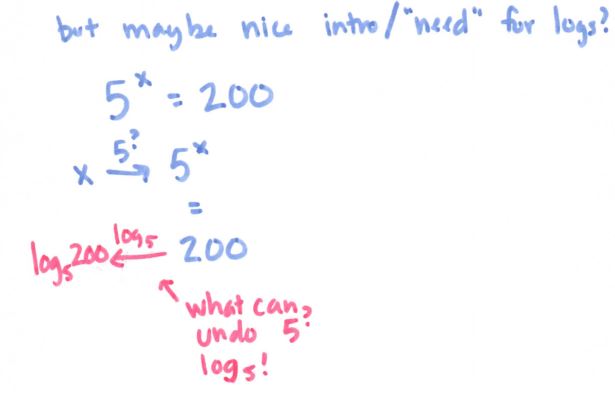
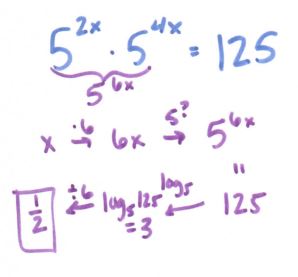
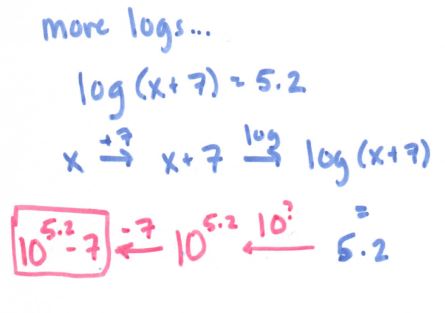
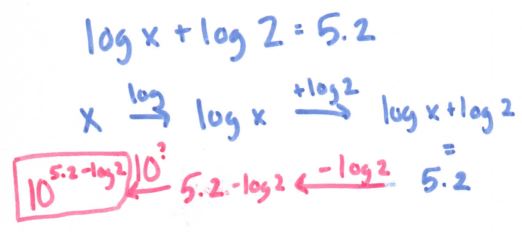
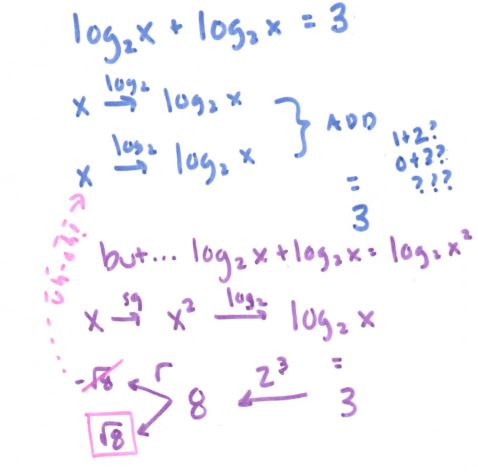
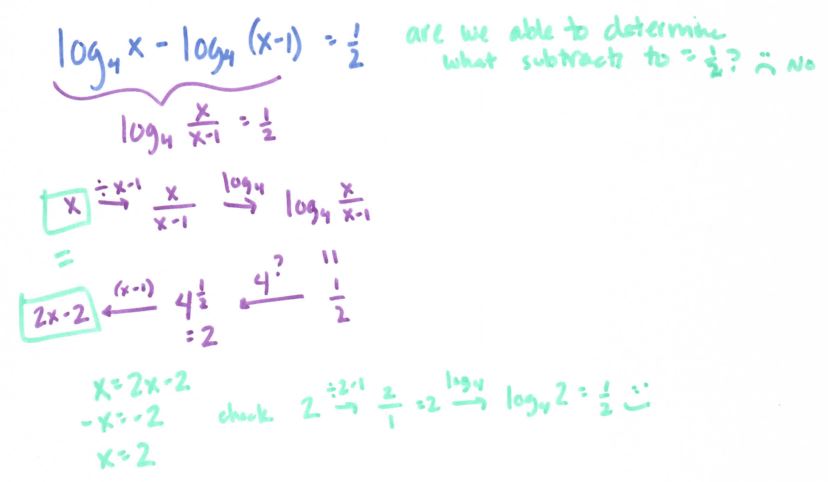
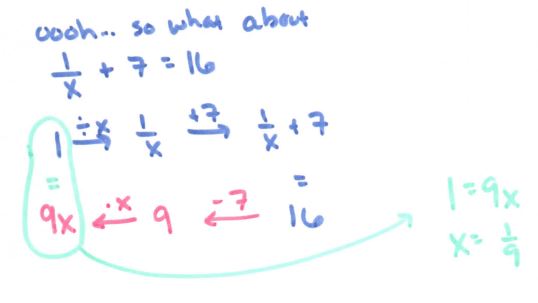
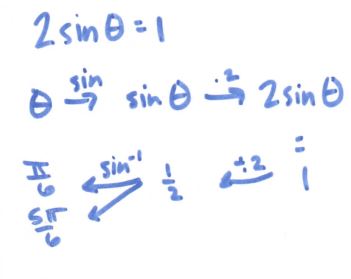
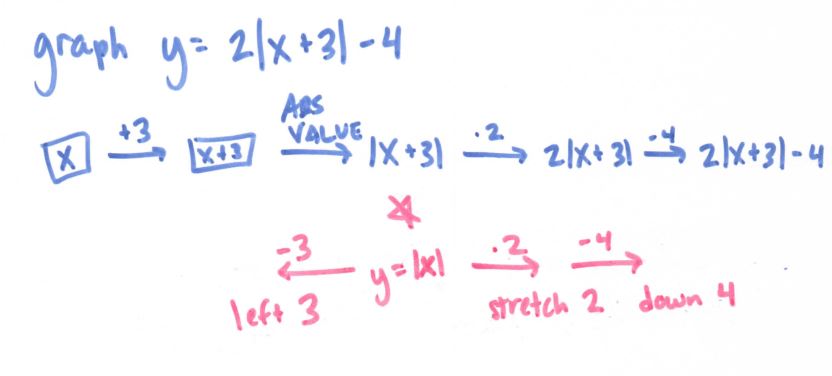

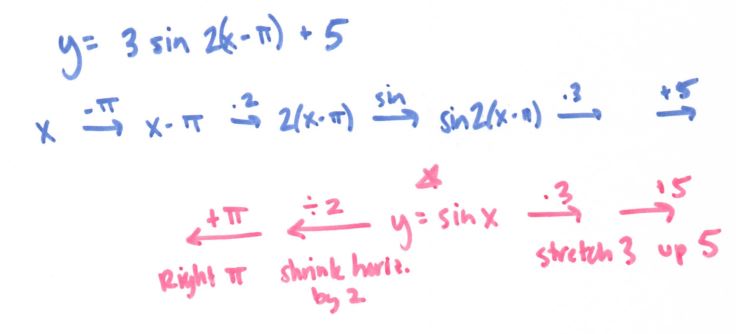

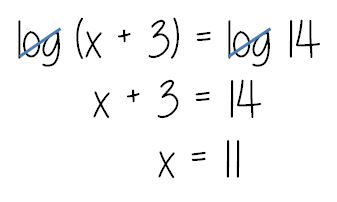
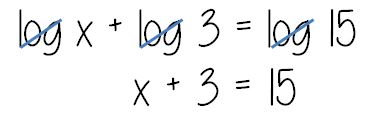
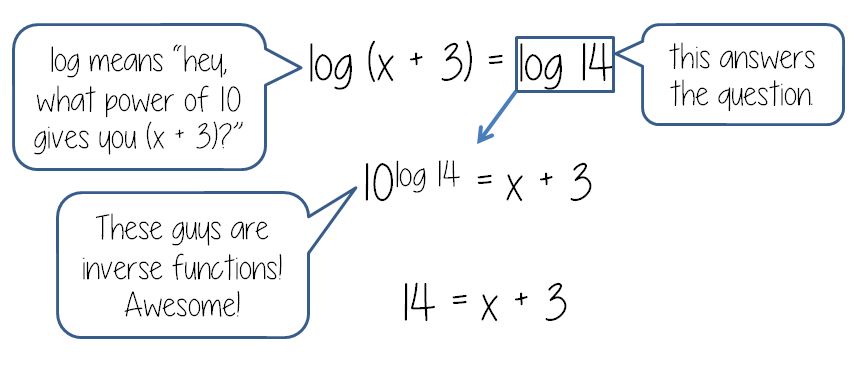

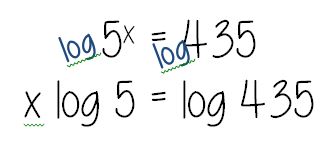
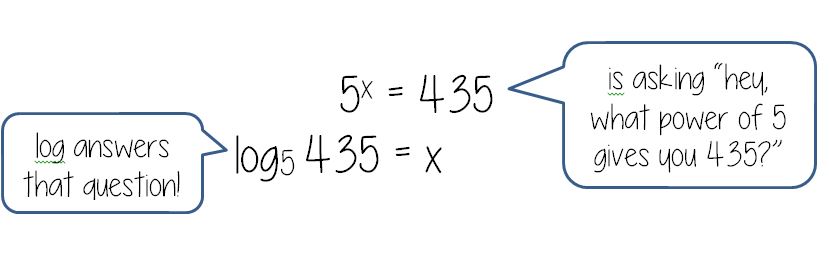


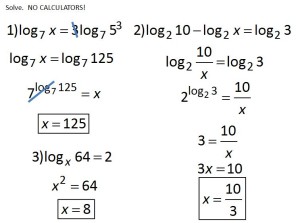
.png/revision/latest?cb=20130322232649)

