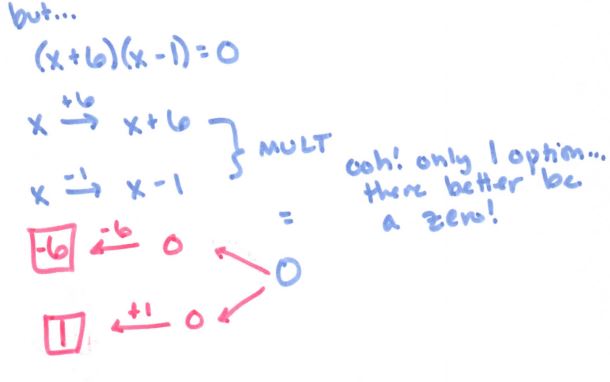
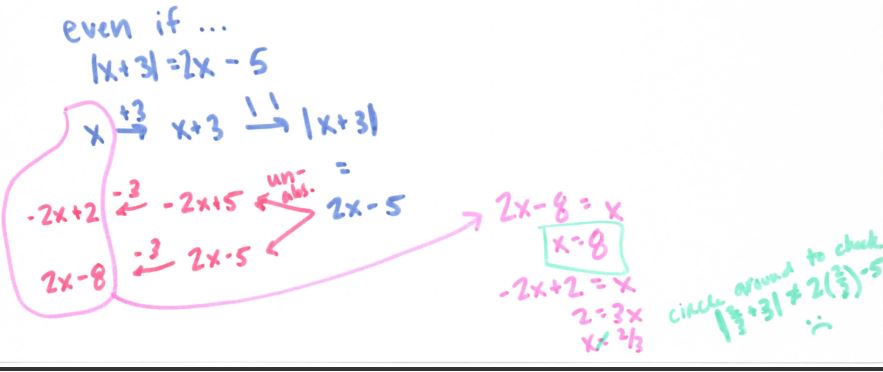
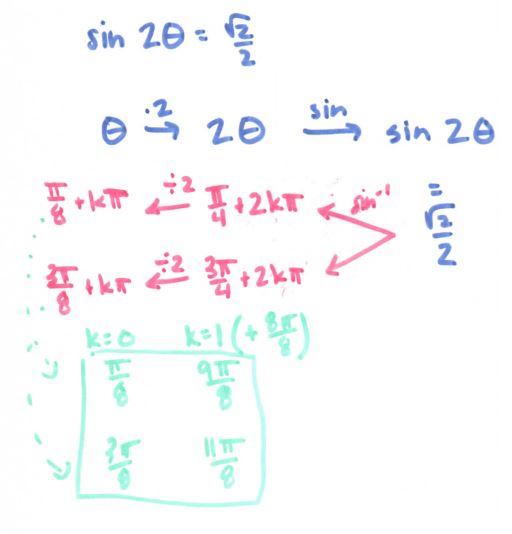
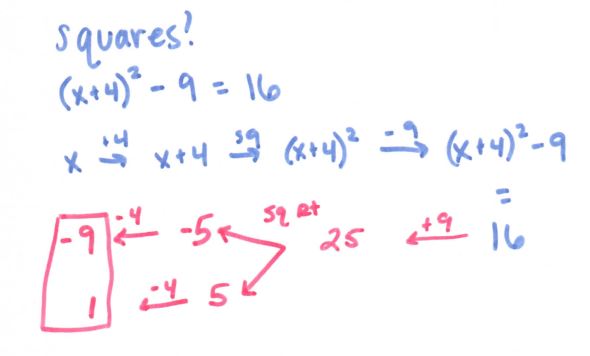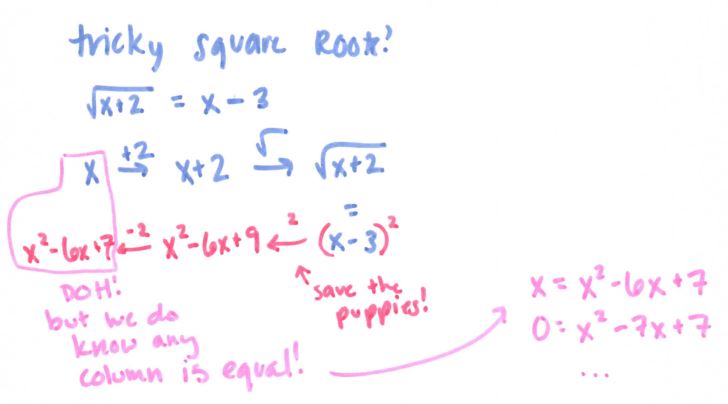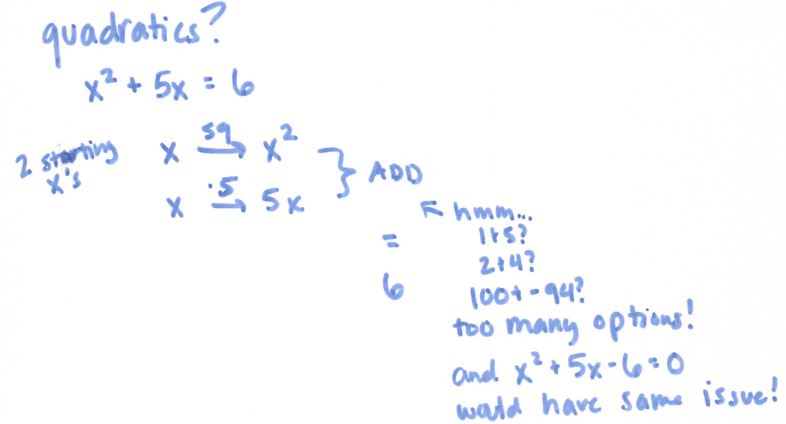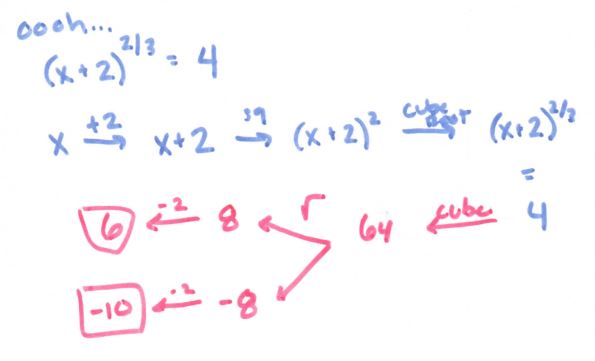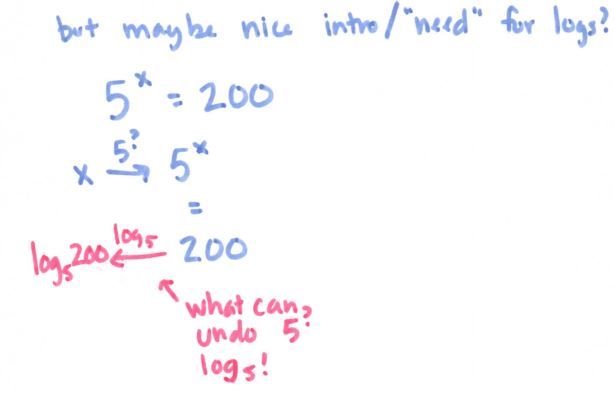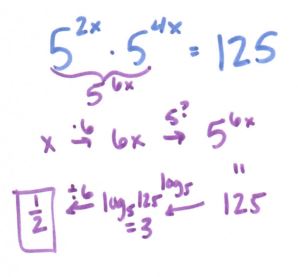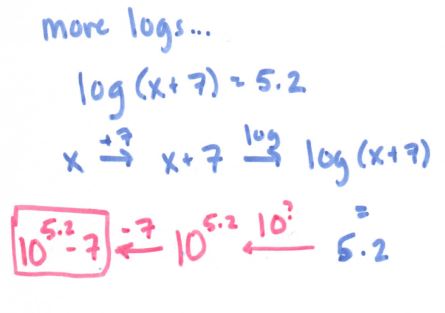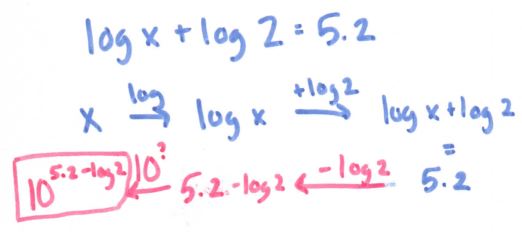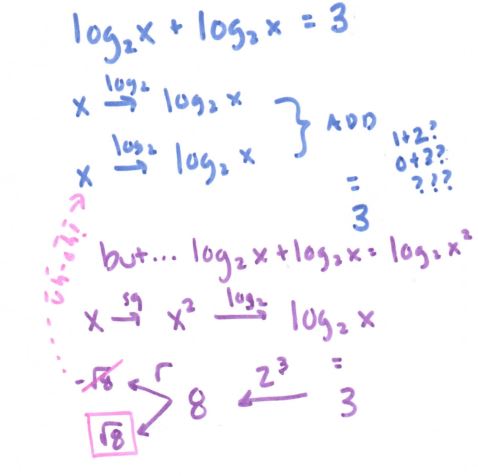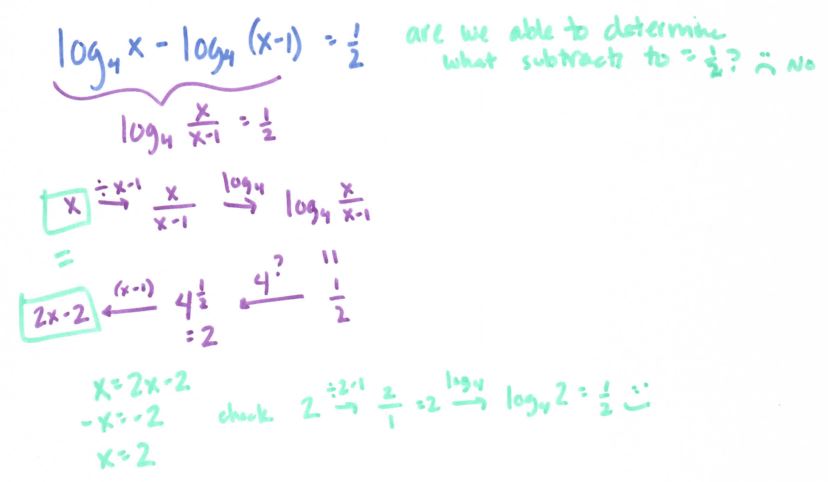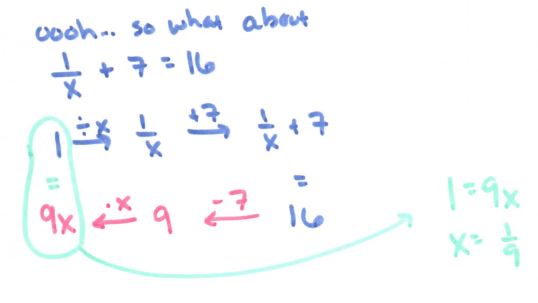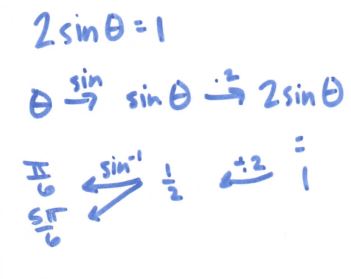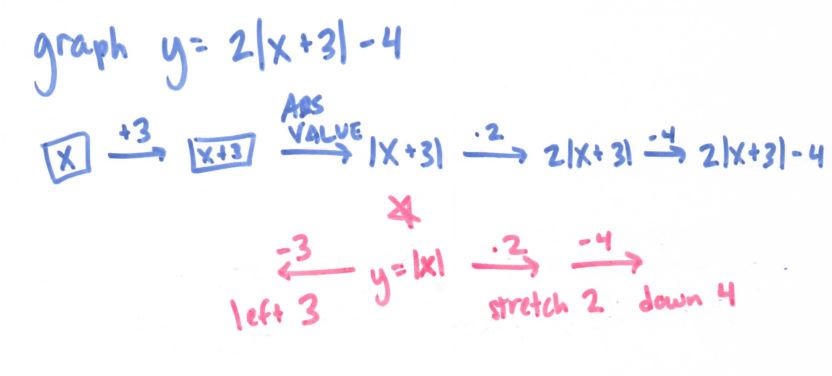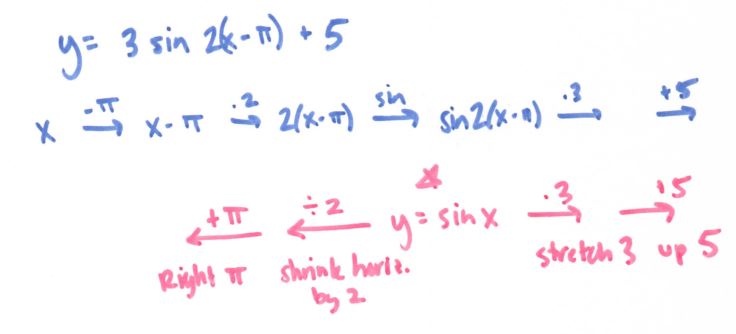See more precal files and FAQs here!
As you may have guess from my TMC presentation, I LOVE function transformations. LOVE LOVE LOVE. So let’s get started with a foldable of parent functions:

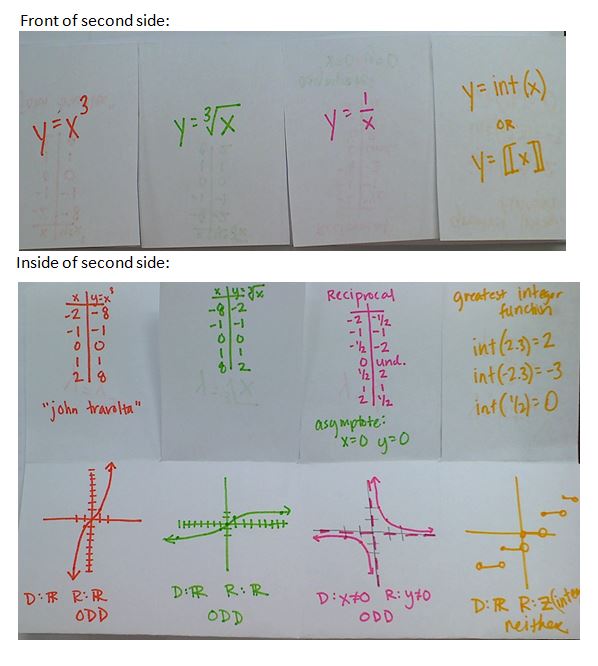 (File with instructions and these pictures here)
(File with instructions and these pictures here)
Homework for the next 3+ days of transformations: (Could someone tell me if that second part is from your blog?!?!)
 (File here). After the first day they have a quiz of sketching the parent functions. I think I may add writing the t-table out as well.
(File here). After the first day they have a quiz of sketching the parent functions. I think I may add writing the t-table out as well.
Then let’s start transforming!
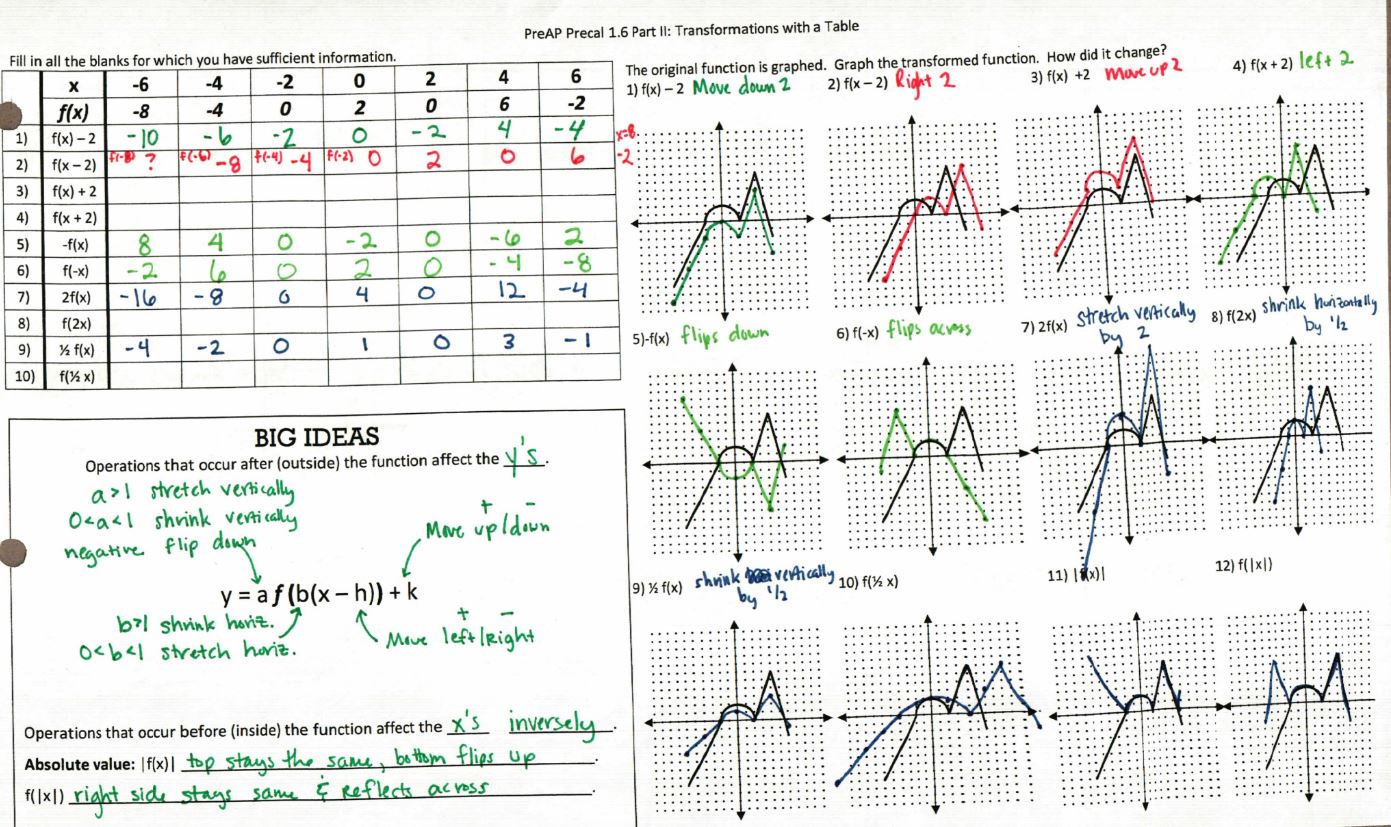 (File here) Also see a more in-depth explanation in this post. And a great post from Shelley! And a great Geogebra app from Jed! SO MUCH AWESOMENESS!
(File here) Also see a more in-depth explanation in this post. And a great post from Shelley! And a great Geogebra app from Jed! SO MUCH AWESOMENESS!
Here’s a practice worksheet:
 I actually had students ASK to make a table like the day before because they could see the transformation easier. I also added these type of questions this year:
I actually had students ASK to make a table like the day before because they could see the transformation easier. I also added these type of questions this year:
There is also a GREAT activity I used that is a bit copyrighted. If you are part of a NMSI/LTF school, look for the “Graphing Transformations” activity. Basically it gave the students a graph in the first quadrant. Then it asked them how the domain/range/max/min/x-values of max/min/x-intercepts/y-intercepts/AROC/area under the curve change based on different transformations. (They told them what the area under the curve was.) It would be really easy to recreate and there was a lot of great thinking and previewing of Calculus in it.
Also STAY TUNED TO THIS BLOG for another great activity to practice writing equations of transformations.
Next up, let’s do transform our parent functions!
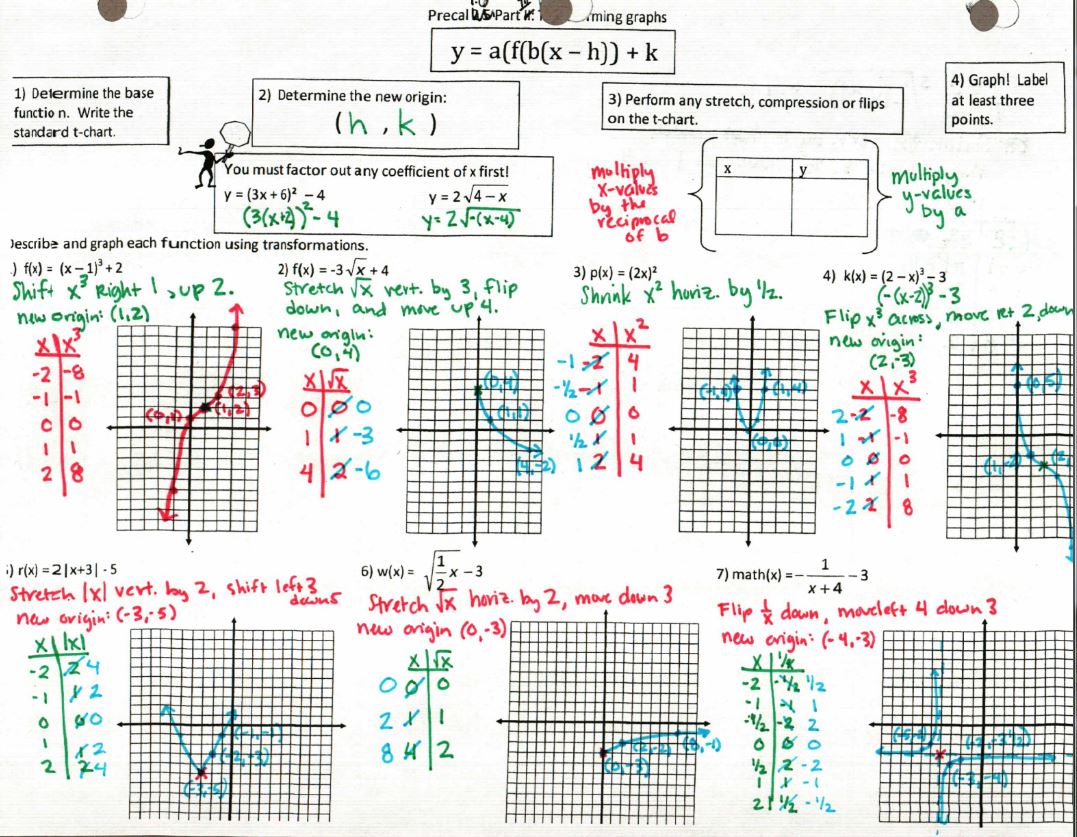
(File here) Read more about this method at the end of this post. The big idea is that we move the ORIGIN (not the “vertex” since not every graph has a vertex) and count our stretched/shrunk graph from our new origin. So easy and beautiful! Works great for conics and trig functions, too!
We did some speed dating practice with it:
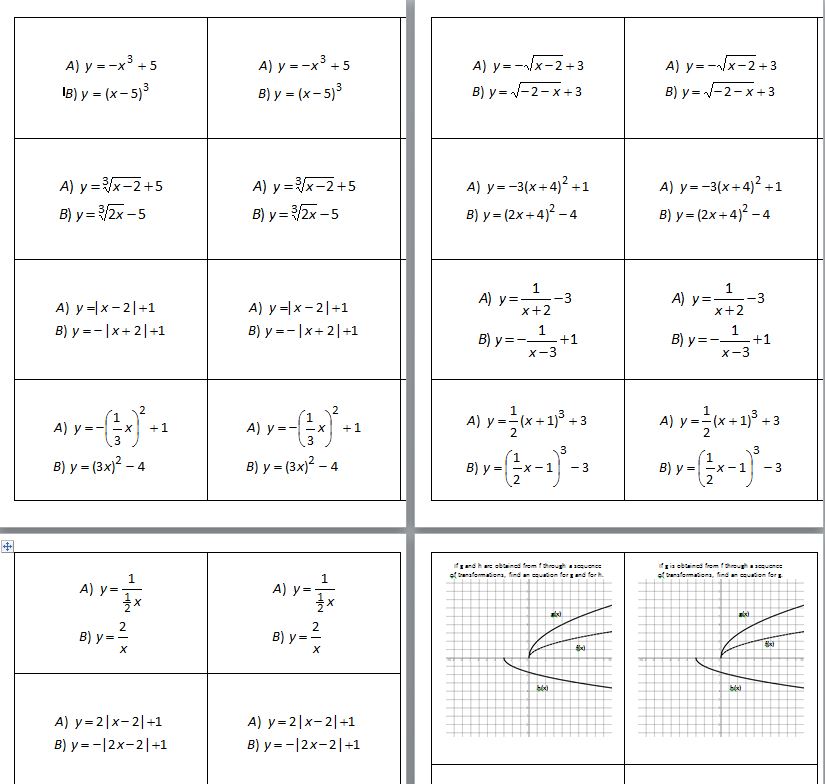
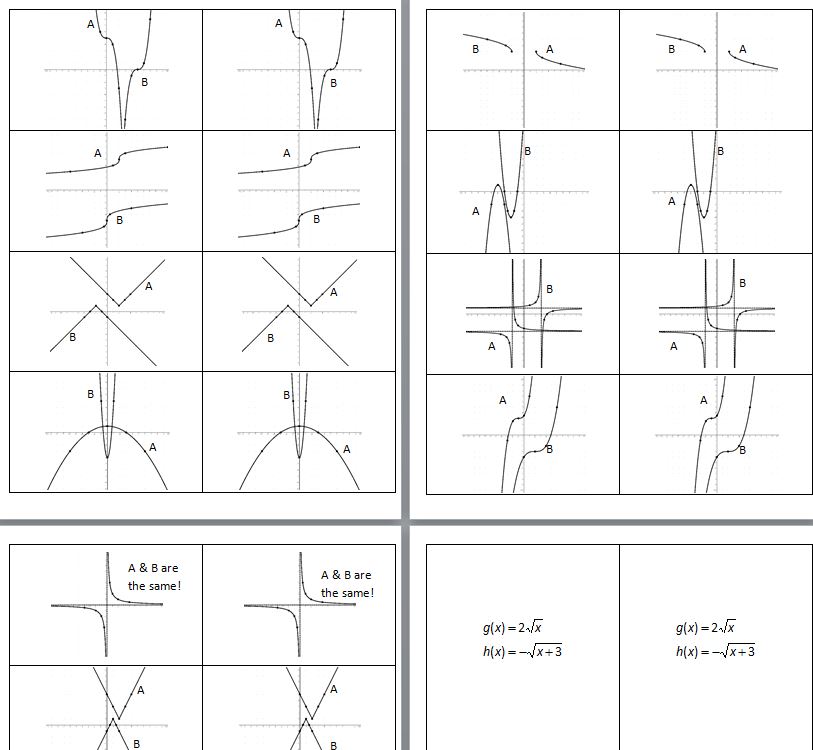 (file here) The first pages are the questions, the second set are the answers. I may change some of them up to make the difficulty more equitable. Some people had really quick graphs and others took a bit longer. Maybe making it so there’s just one hard one, but two easy ones? I’ll let y’all sort that out and get back to me.
(file here) The first pages are the questions, the second set are the answers. I may change some of them up to make the difficulty more equitable. Some people had really quick graphs and others took a bit longer. Maybe making it so there’s just one hard one, but two easy ones? I’ll let y’all sort that out and get back to me.
So after what seems like forever (yet not enough time), we move onto function compositions:
 (file here) Things to notice: I write the outside function first, putting ( ) wherever there is an x. Then plug in the inside function into those parentheses, leaving a ( ) wherever there’s an x in that function. Then plug in the value. This seemed to go a lot smoother than finding g(5), then plugging that into f, especially if you have a composition of more than 2 functions, or if you have 2 x’s in the “outside” function. Also, notice that cool way of simplifying the complex fractions on #4. Read more about it here.
(file here) Things to notice: I write the outside function first, putting ( ) wherever there is an x. Then plug in the inside function into those parentheses, leaving a ( ) wherever there’s an x in that function. Then plug in the value. This seemed to go a lot smoother than finding g(5), then plugging that into f, especially if you have a composition of more than 2 functions, or if you have 2 x’s in the “outside” function. Also, notice that cool way of simplifying the complex fractions on #4. Read more about it here.
Homework:  (file here)
(file here)
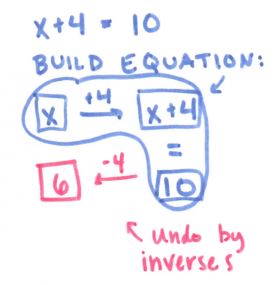
Then some inverses. I want to do A LOT more with them this year and start talking about them WAY EARLIER (See my flowchart epiphany here). But here’s what I did last year:
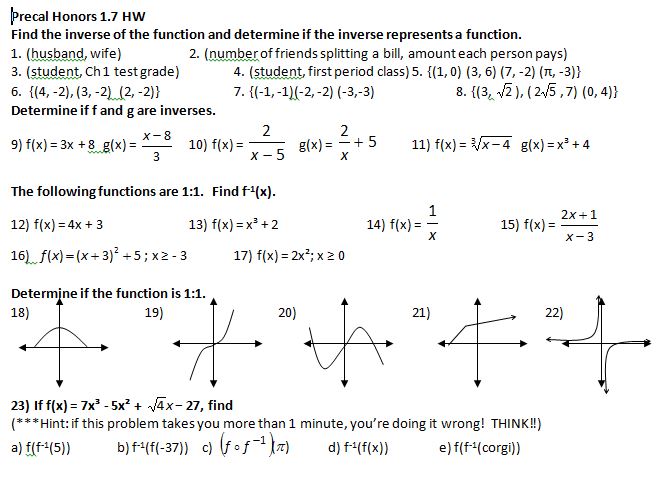 (file here) (yes, even though it says 1.7 instead of 1.8 at the top. Numbers are hard.)
(file here) (yes, even though it says 1.7 instead of 1.8 at the top. Numbers are hard.)
And a really good in-class sheet with some practice Free Response Questions:
And then it’s study guide day!
Now go forth and transform.