People, this post is why I love the #MTBoS. You can’t read everything, learn everything, critically think about everything; but if you read blogs and tweets, then you can collect more of that knowledge than you would alone. So even though I am not participating in the #intenttalk book study/chat (Am I the only one who always thinks it’s Kimmie Schmidt on the cover?), I did see this tweet from Bridget:
Curious–> what does #intenttalk thinks abt comparing and connecting these two methods pic.twitter.com/OXHglnvE7P
— Bridget Dunbar (@BridgetDunbar) July 1, 2015
I used that method a wee bit this year when I taught inverse functions and a few students really latched onto it. But now I’m thinking of starting this way on day one, building on it, and tying it into Glenn’s three rules of mathematics. I sat down and played with it a bit for the last few days and all I can say is:

Are you ready for this? Ok, let’s just dip our toes in:
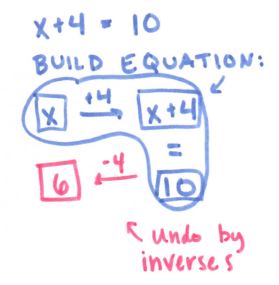 The main idea being that we think through the equation “forwards” and then work back to the solution using inverses. Another easy one:
The main idea being that we think through the equation “forwards” and then work back to the solution using inverses. Another easy one:
 I like (a) completing the circle of life by checking our answer and (b) each column showing equal values.
I like (a) completing the circle of life by checking our answer and (b) each column showing equal values.
How about we try out the shallow end:

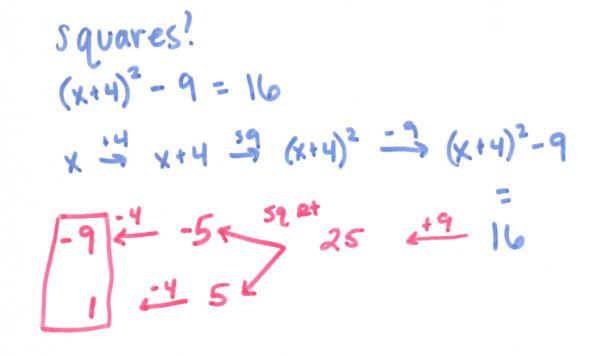 Yeah, I’m totally digging the two arrows for square root, too.
Yeah, I’m totally digging the two arrows for square root, too.
 Are your ready to put your head underwater? Ok, here it is….wait for it…
Are your ready to put your head underwater? Ok, here it is….wait for it…
So one place where this method has problems is if there are variables on both sides. But I want to use this more as an introduction in each section, not a method for solving each individual equation. However, we can use the fact that each column is equal to set up the rest of the problem and finish with quadratic formula.
Now I thought for sure this could not work with quadratics. OR COULD IT?

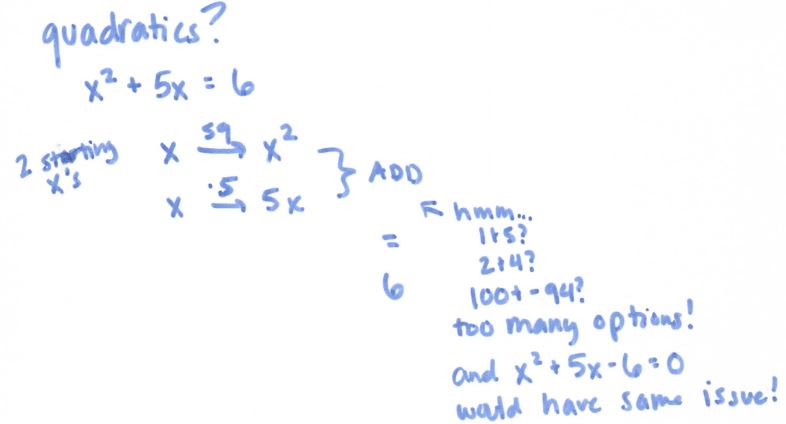 Ok, so the weird thing here is that (a) my new erasable markers don’t like it when you rewrite over something you just erased and (b) we have 2 places that x is involved, so 2 starting points. But then I don’t know how they are going to add to equal 6. But (spoiler alert!) we do know what has to happen if we’re going to multiply to equal zero…
Ok, so the weird thing here is that (a) my new erasable markers don’t like it when you rewrite over something you just erased and (b) we have 2 places that x is involved, so 2 starting points. But then I don’t know how they are going to add to equal 6. But (spoiler alert!) we do know what has to happen if we’re going to multiply to equal zero…
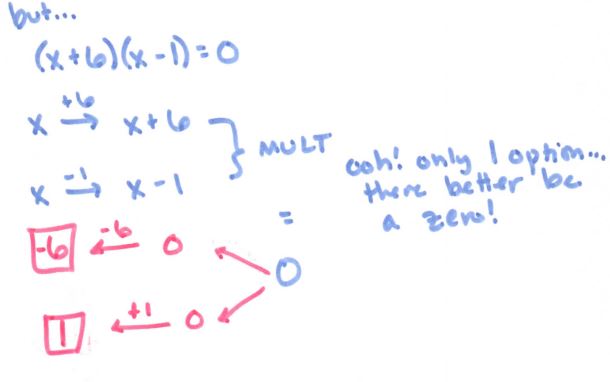 Here the two back arrows from zero come from the fact we had two x inputs. Pretty powerful, eh? Let’s try it on some other tricky problems, like rational exponents:
Here the two back arrows from zero come from the fact we had two x inputs. Pretty powerful, eh? Let’s try it on some other tricky problems, like rational exponents:
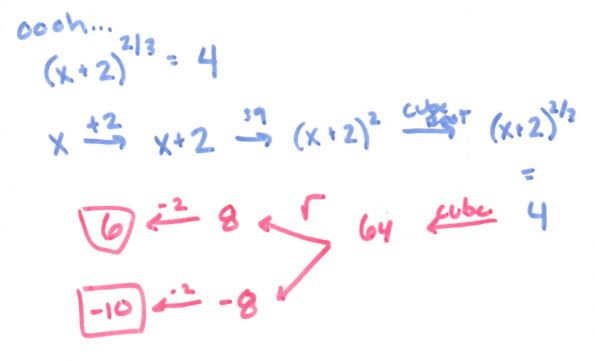 Ok, guys, we’re going to jump into the deep end now….ABSOLUTE VALUE!
Ok, guys, we’re going to jump into the deep end now….ABSOLUTE VALUE!

Update: I was so excited about “un-absolute valuing” that I forgot to “un-multiply”. -6 should turn into 3, which would then turn into -3 and 3; and finally -6 and 0 as the answers. Which I probably would have noticed if I followed my own recommendation to circle back through.
Holy cow I’m in LOVE LOVE LOVE with having to “unabsolute value” as a step, because of course to “unabsolute value” you go back to positive or negative.
But wait, what about….
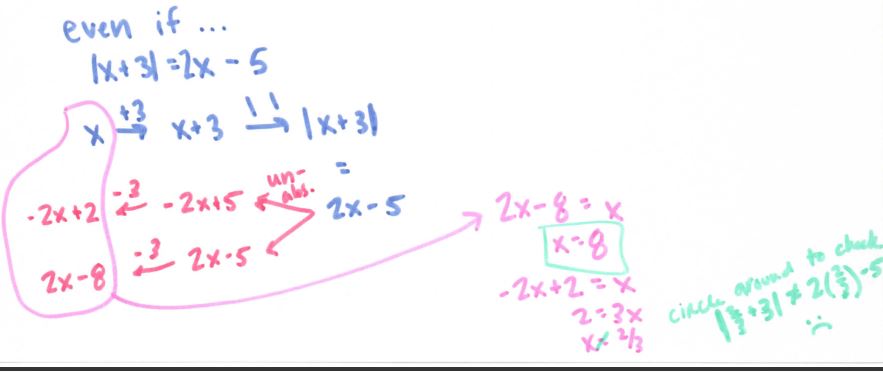 Ok, ok, a little tricky, but not undo-able.
Ok, ok, a little tricky, but not undo-able.
Now I did have trouble with this problem:
 I wasn’t sure if my beginning value should be x or 5. When I tried it with 5, I thought of it as “If I’m at 125, what root would I need to get to 5? Oh, the third root. That means the original operation in the top line needs to be the inverse of the third root, which is cubing, which means x = 3.”
I wasn’t sure if my beginning value should be x or 5. When I tried it with 5, I thought of it as “If I’m at 125, what root would I need to get to 5? Oh, the third root. That means the original operation in the top line needs to be the inverse of the third root, which is cubing, which means x = 3.”
But if I keep my beginning value as x, then it leads into a nice intro/need for logs:
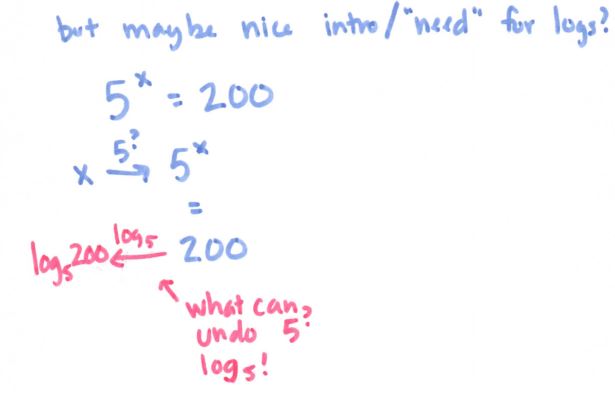 And then I went crazy with the log problems! (Although not pictured is two logs equal to each other, e.g. log (x + 7) = log (2x – 4). I’ll leave it as an exercise for the reader; it really is quite pretty.)
And then I went crazy with the log problems! (Although not pictured is two logs equal to each other, e.g. log (x + 7) = log (2x – 4). I’ll leave it as an exercise for the reader; it really is quite pretty.)
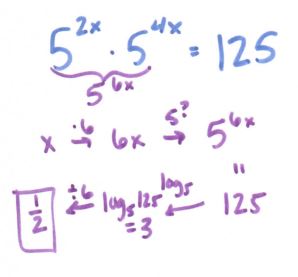
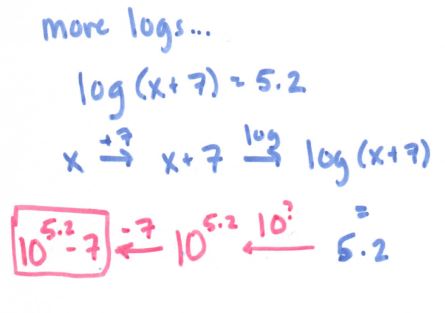
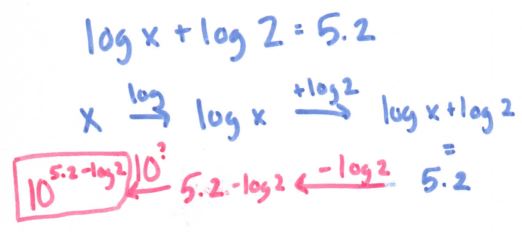
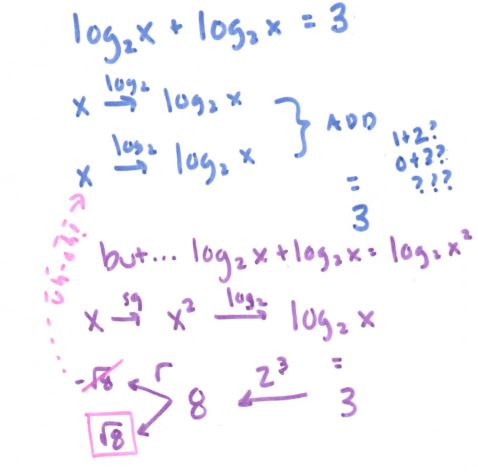 The last one being another case of, “Uh-oh, need to rewrite this as something isn’t so ambiguous.” Another case of that:
The last one being another case of, “Uh-oh, need to rewrite this as something isn’t so ambiguous.” Another case of that:
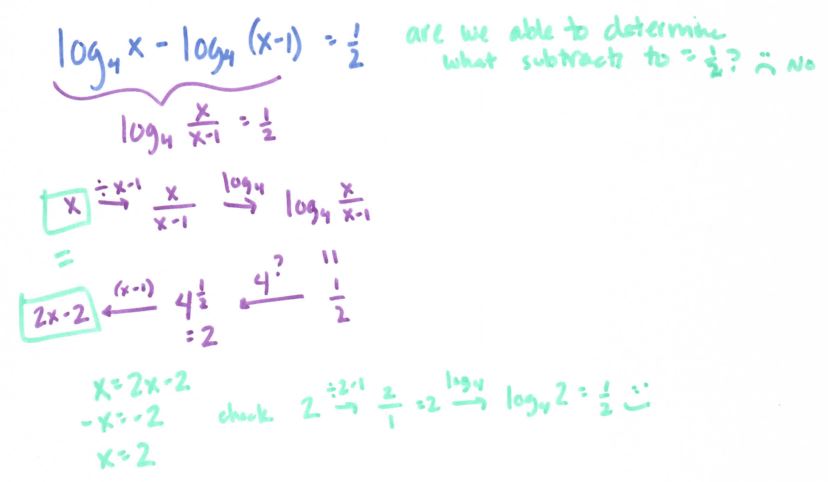 Ok, ok, I don’t know why I didn’t have two starting x’s and then divide them, but isn’t it just beautiful how it works out this way? So I went some more down that path:
Ok, ok, I don’t know why I didn’t have two starting x’s and then divide them, but isn’t it just beautiful how it works out this way? So I went some more down that path:
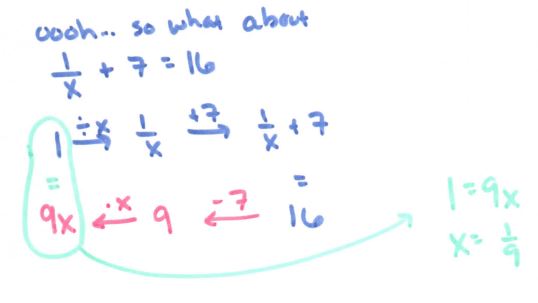 Then I thought of other problems that cause students anguish, and immediately thought of the difference between 2sin(x) and sin(2x):
Then I thought of other problems that cause students anguish, and immediately thought of the difference between 2sin(x) and sin(2x):
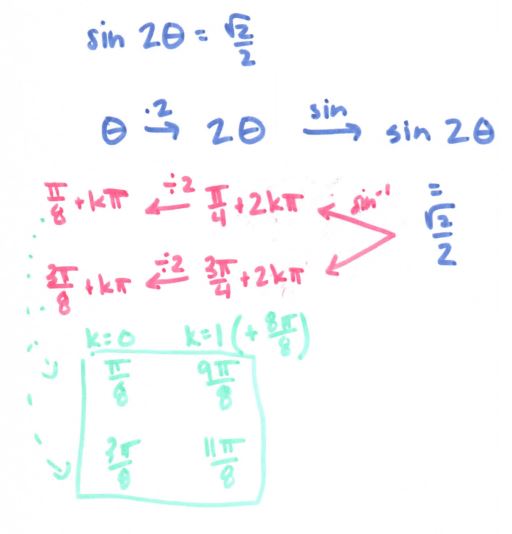
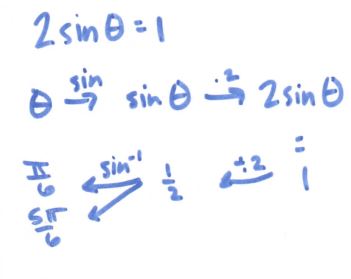 After this, my brain was pretty much done for the day. Or at least, I thought it was. Then I had a shower thought (where all problems are solved): hey, wonder if I could tie it to graphing transformations?
After this, my brain was pretty much done for the day. Or at least, I thought it was. Then I had a shower thought (where all problems are solved): hey, wonder if I could tie it to graphing transformations?
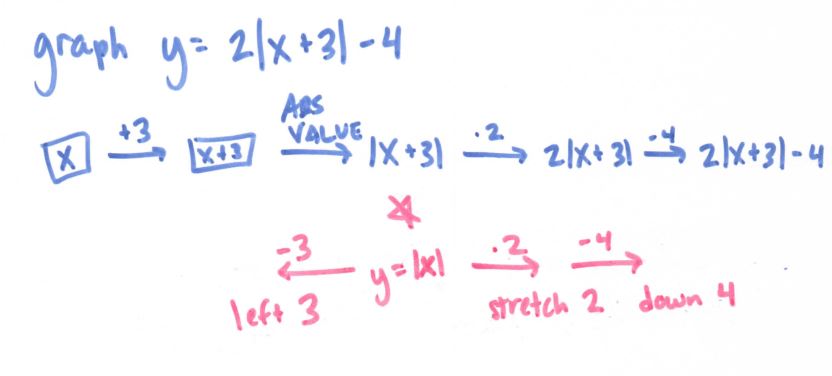 GAH!!!!! So you go through all the steps, then find your parent function, in this case absolute value. You have to use inverses to get to x (minus three, or in this case three to the left) and OH I SHOULD HAVE PUT = Y AT THE VERY END BECAUSE THEN YOU TRAVEL “FORWARD” (stretch 2, down 4) FROM THE PARENT FUNCTION TO GET TO Y.
GAH!!!!! So you go through all the steps, then find your parent function, in this case absolute value. You have to use inverses to get to x (minus three, or in this case three to the left) and OH I SHOULD HAVE PUT = Y AT THE VERY END BECAUSE THEN YOU TRAVEL “FORWARD” (stretch 2, down 4) FROM THE PARENT FUNCTION TO GET TO Y.

Another one? ANOTHER ONE!
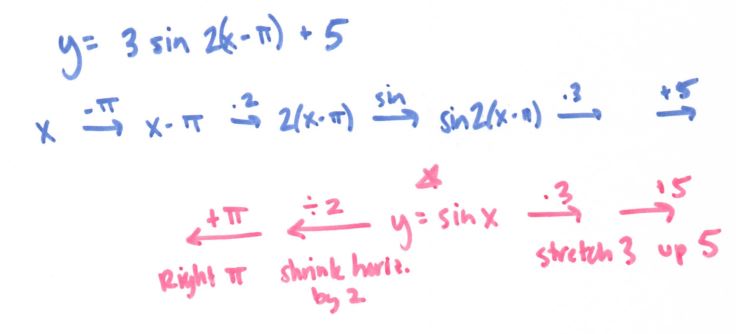 I don’t know why you would want it, but if you did want all of these examples in one pdf, here you go. Now there are some drawbacks as I’ve mentioned: things need to be simplified first, somethings get a little wonky, how will this work for trickier equations; but I think Kayne sums it up pretty nicely:
I don’t know why you would want it, but if you did want all of these examples in one pdf, here you go. Now there are some drawbacks as I’ve mentioned: things need to be simplified first, somethings get a little wonky, how will this work for trickier equations; but I think Kayne sums it up pretty nicely:

Would love any thoughts/opinions/comments/suggestions/epiphanies!
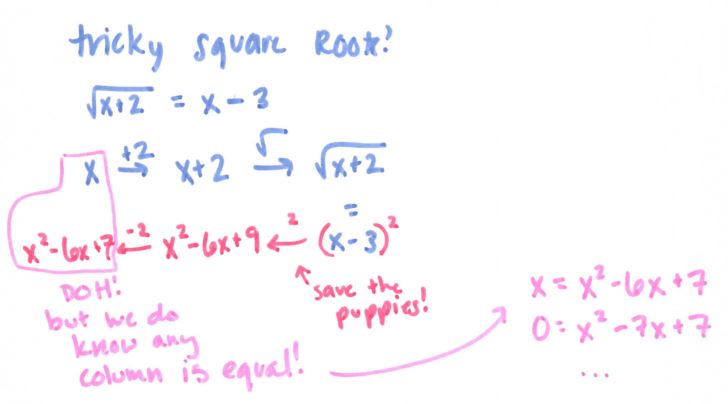
Carl
July 6, 2015 at 8:30 am
This totally made my day. Then I felt really sad.
When I thought ninth grade I remember telling kids to stop using this picture method that they love because in order to do more sophisticated math they’ll need to learn the “stack” method, as if this picture method only works for two step equations. Now I know that this method could be used as a way to help all kids really understand the fundamental rules of math. Awesome!
Meg Craig
July 6, 2015 at 8:46 am
I’m guilty of making them do “big people” math, too, when “common sense” math would work just as well. Now you can tell the kids that they were right, and they’ll love to hear that!
The Flowchart Method: Learn It, Love it, Log it. – Insert Clever Math Pun Here
March 31, 2016 at 1:42 pm
[…] readers of my blog may remember my ramblings of the “flowchart method” last summer (and my use of it at the start of the year in Algebra II). After not focusing on […]
Jennifer Kelly
April 21, 2017 at 7:06 am
Thank you for posting this. I found this post over the summer and used this method for solving equations with variables on one side and for finding inverses. My students are in a class called algebraic reasoning, which is a bridge course between algebra 1 and algebra 2. They have been extremely successful using this method.
Meg Craig
May 8, 2017 at 8:33 pm
Awesome!! I am so glad this helped your students be successful and I’m so glad you let me know!
Krystle Brown
September 13, 2018 at 12:43 pm
This post was so helpful. Thank you! I tried showing my kids the do/undo method and it left them more confused. This was really helpful and I think will make a big difference when I show them the flowchart method.
Meg Craig
January 1, 2019 at 9:24 am
You are very welcome! I hope it helped!!