(The continuation of my posting all of my resources for Algebra II. See more files and FAQs here.)
So the students have seen lines in middle school, Algebra I, and Geometry, so this should be a nice easy review, right? “Hey guys, let’s graph a line! And then let’s start in point-slope form and write an equation of a line!”
Until they find a cure for Math Amnesia, I guess we’ll start from scratch! Starting with functions:
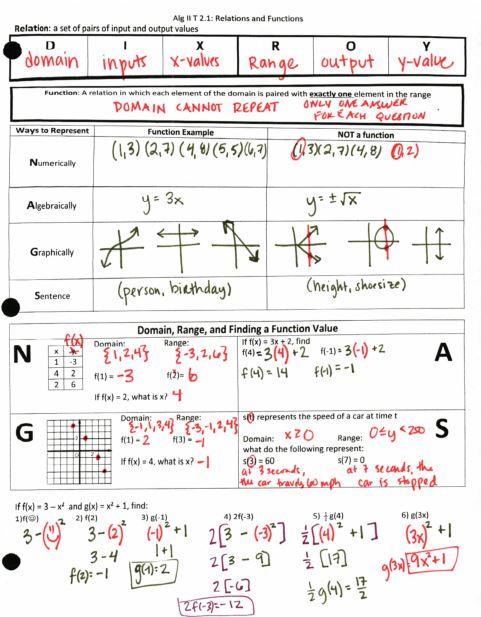File here. (sorry for the some wonkiness in the scans… I use a roller scanner. If my phone had any sort of storage/wifi/3Gsignal in school, I’d use CamScanner instead, but alas..) Next year I’ll be sure to use the vending machine analogy that Justin (@JustinAion) shared on twitter:
And some homework:
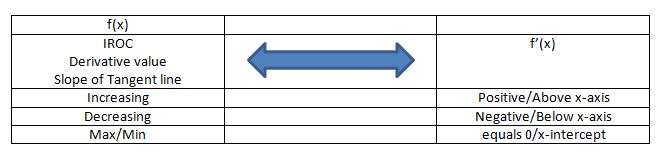
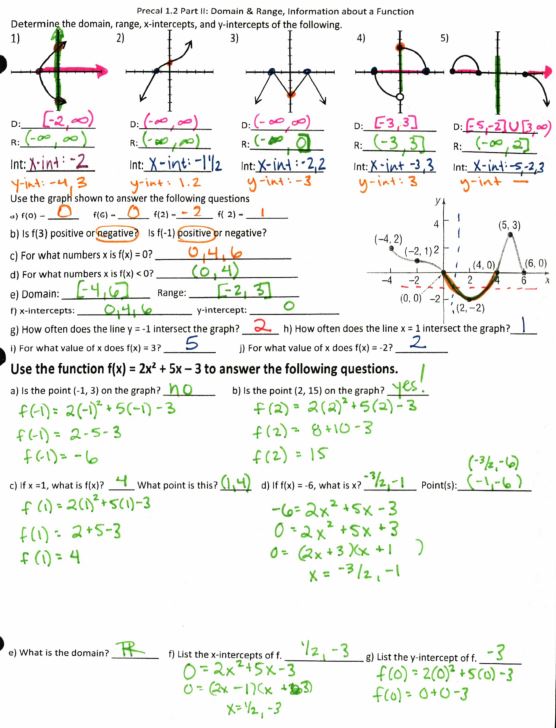
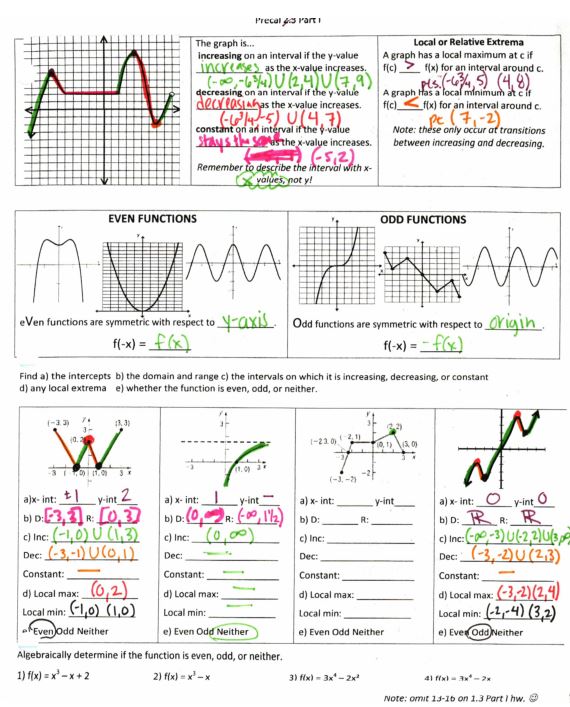
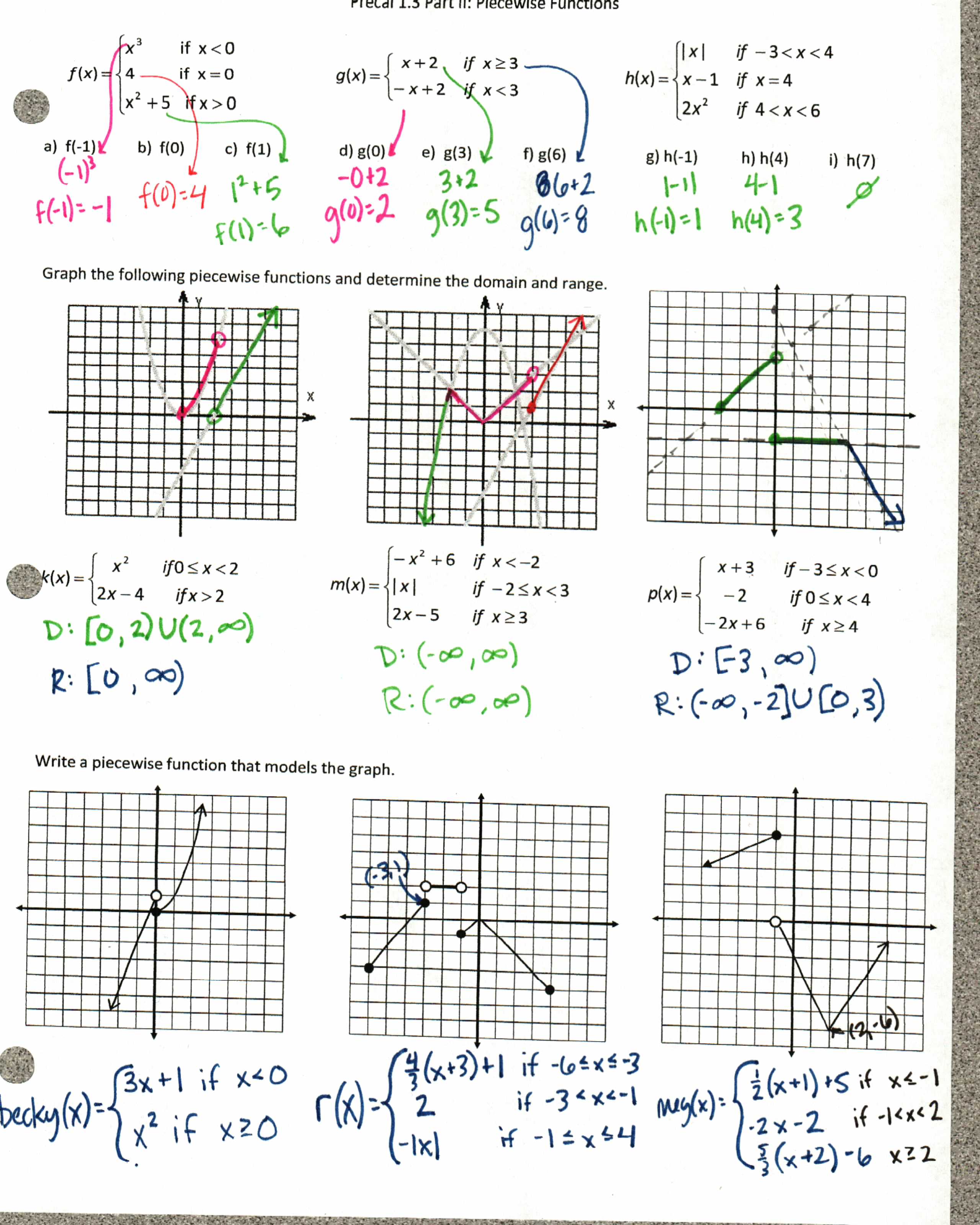
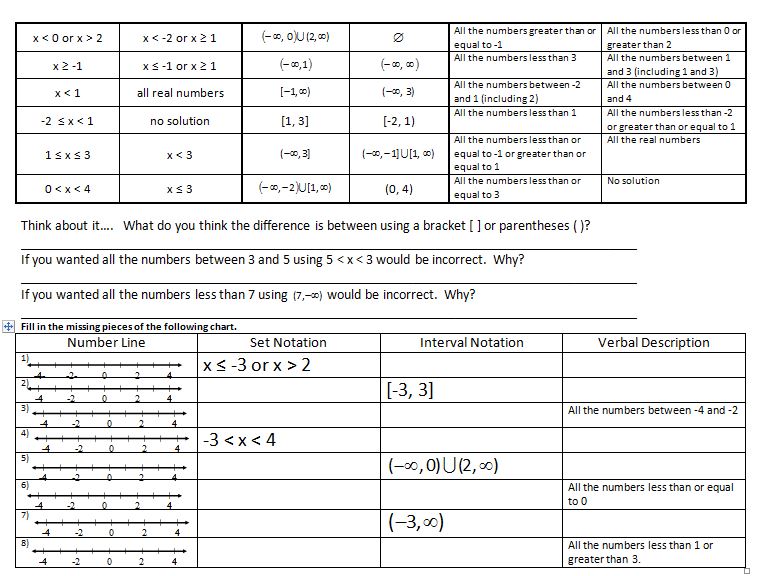
What is it about domain and range that students have such a hard time with it? As you can see, I try both the “flatten the graph to the x or y axis” method and the “box in your graph” method.
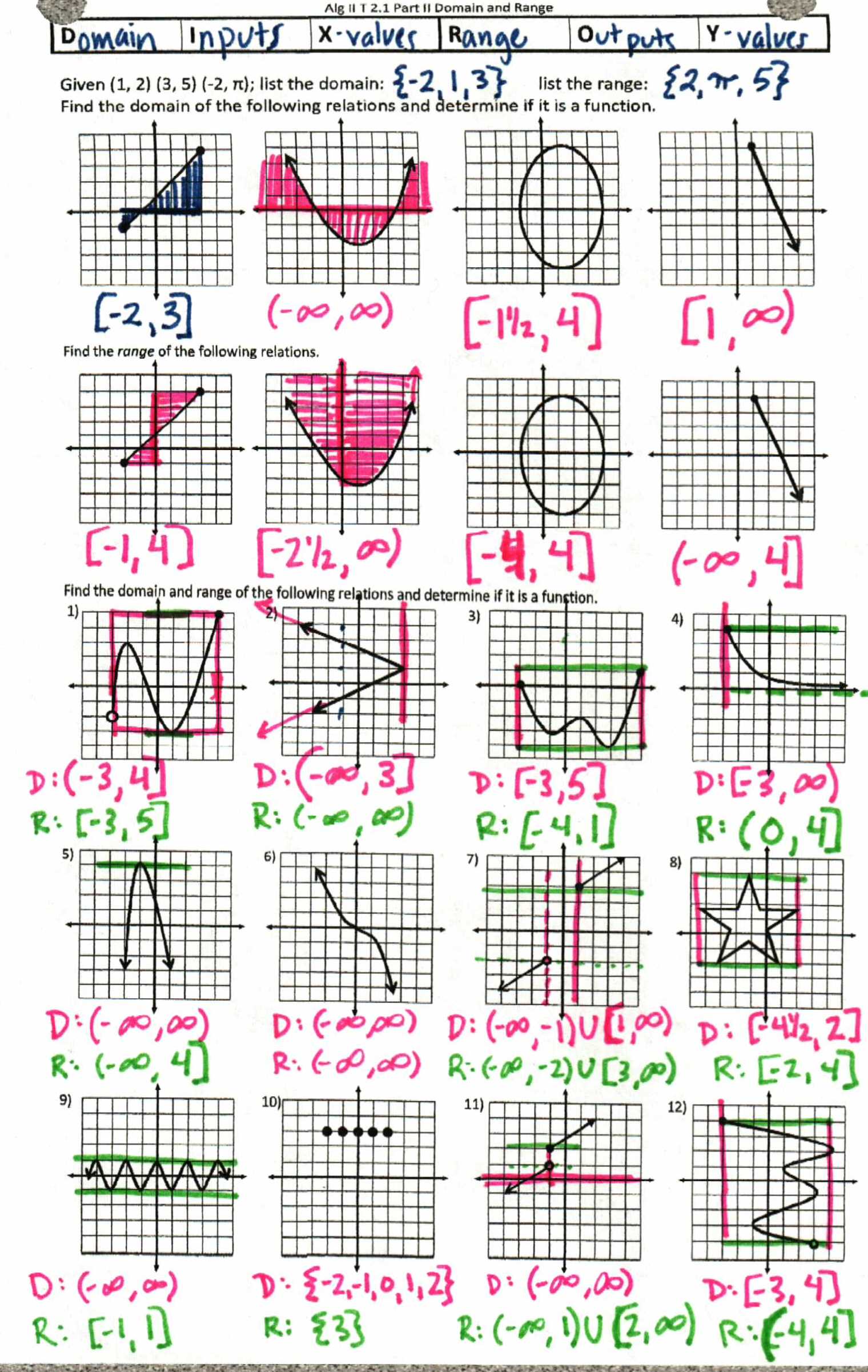File here. (Legal, but it’s sized to shrink to 2/letter sized).
Somewhere about this time, I like to do graphing stories:
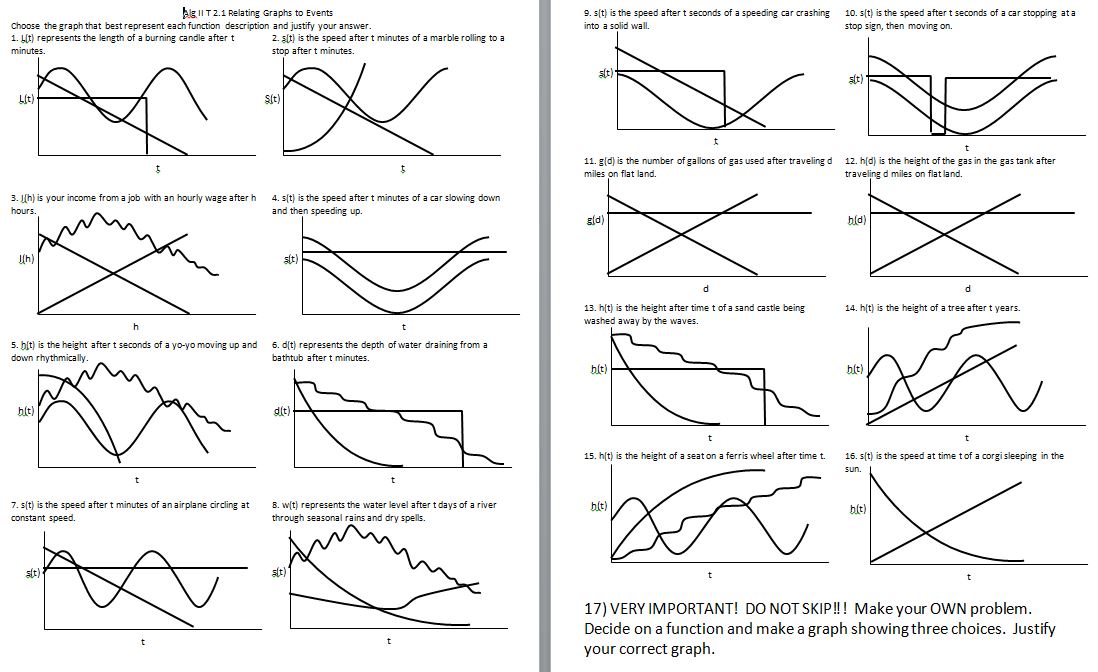File here (not my original idea, I just made it into a worksheet instead of card sort). Also, yeah, #6 always gets me. I want to say it’s the curved line, but only by process of elimination. I’ll have to do some filming of a bathtub one day.
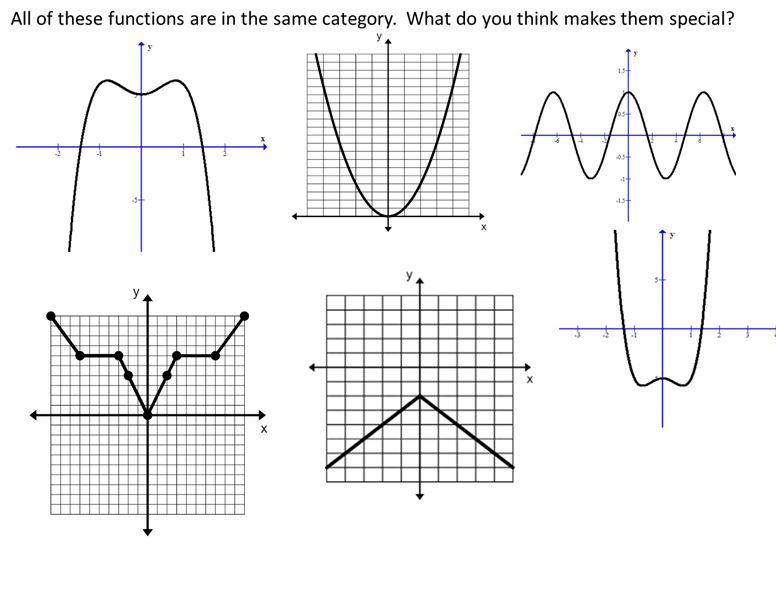
However, I think I’d like to replace it with this graph matching instead:
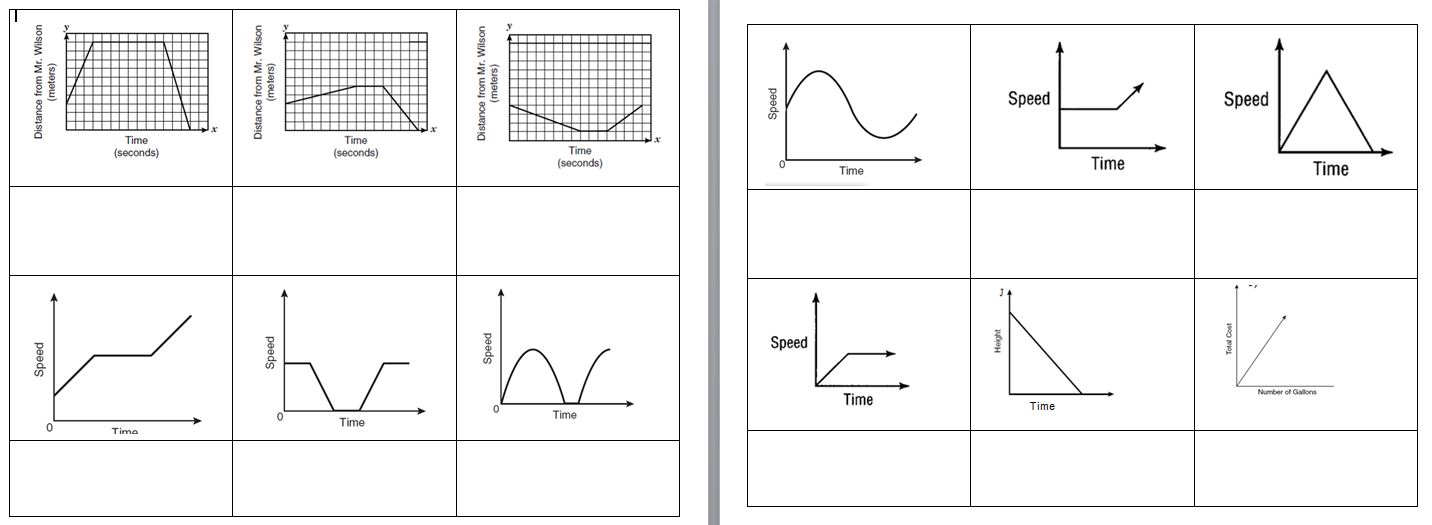
File here. Again, not mine and I haven’t tried it yet, but it seems a little bit higher level.
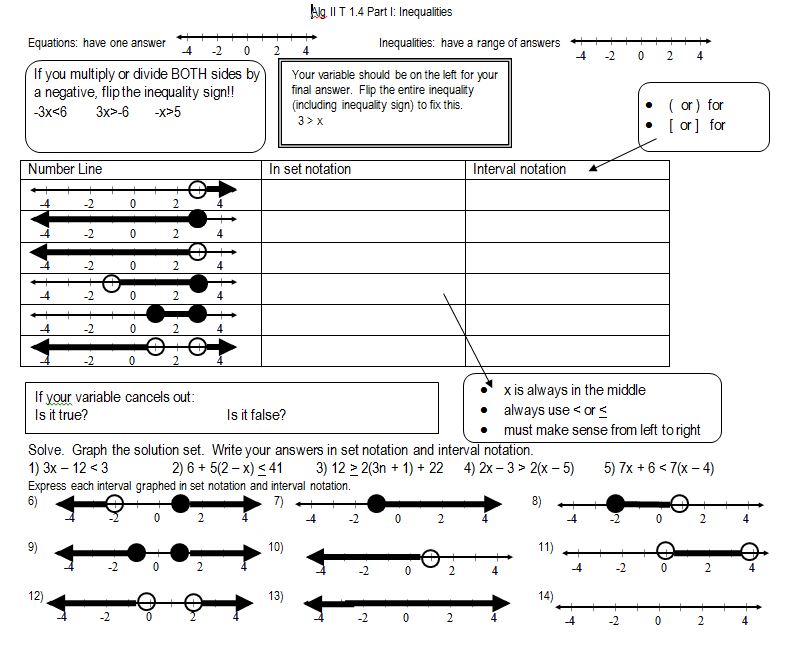
Ok, now it’s time to get started with those lines!
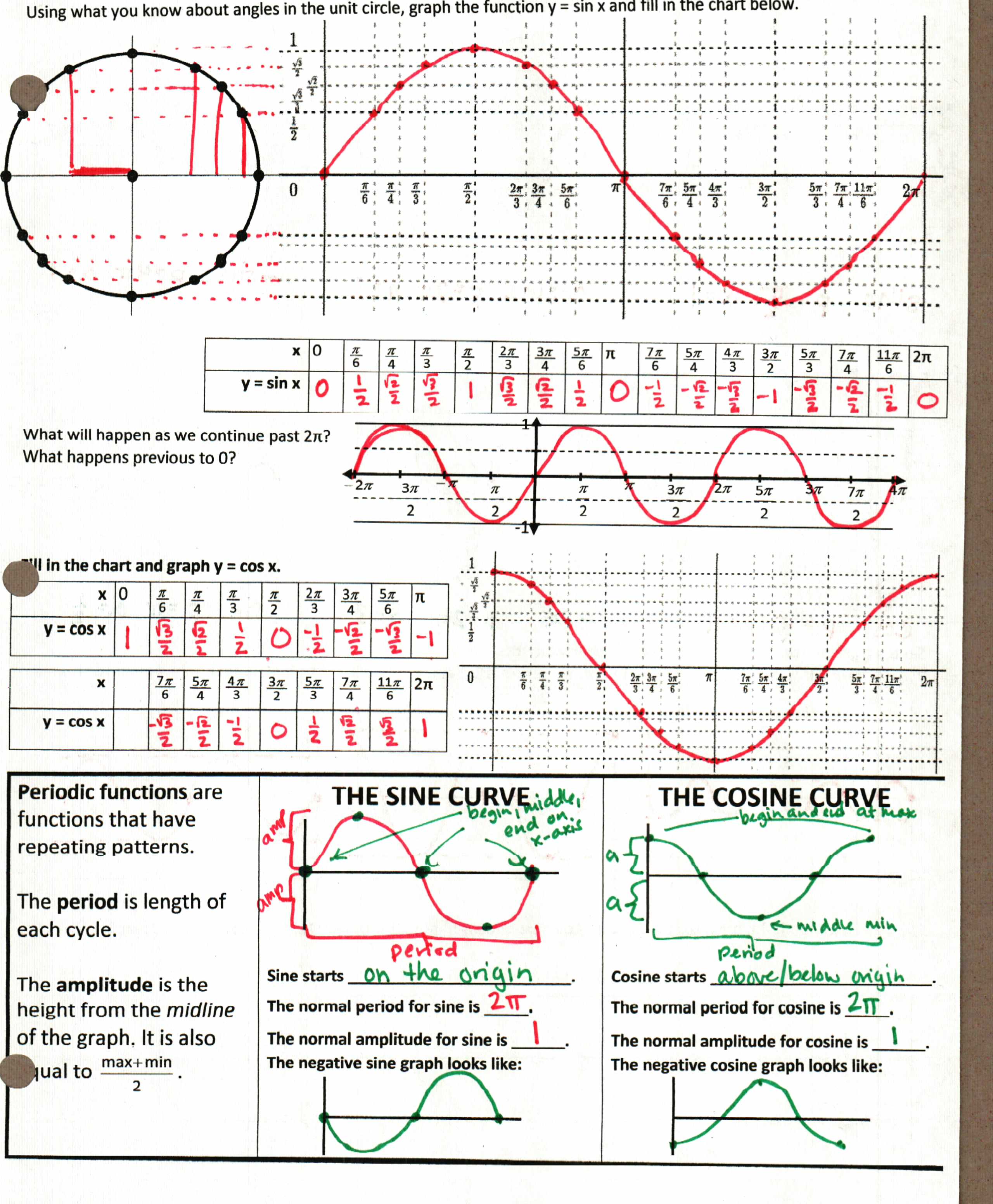
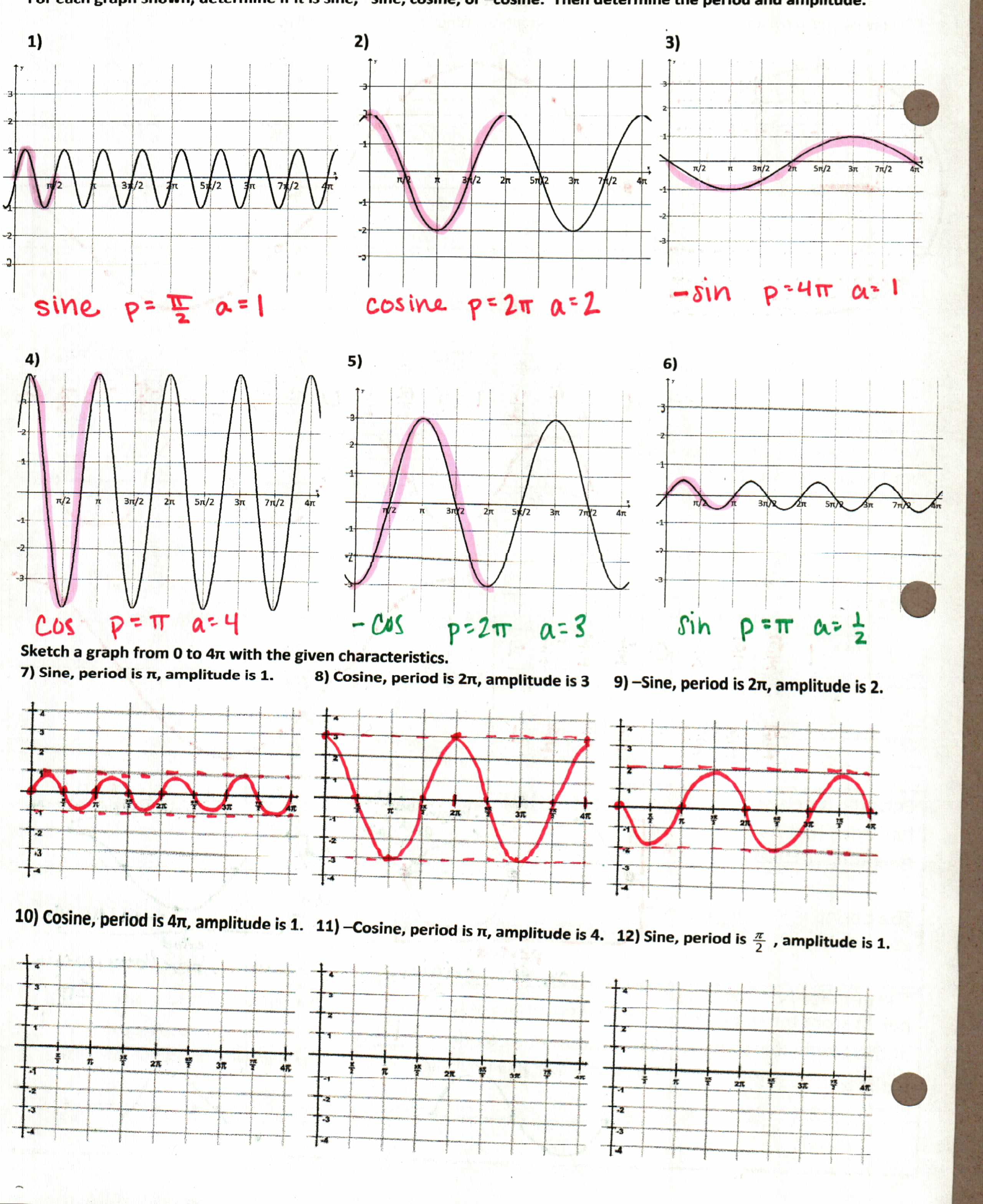
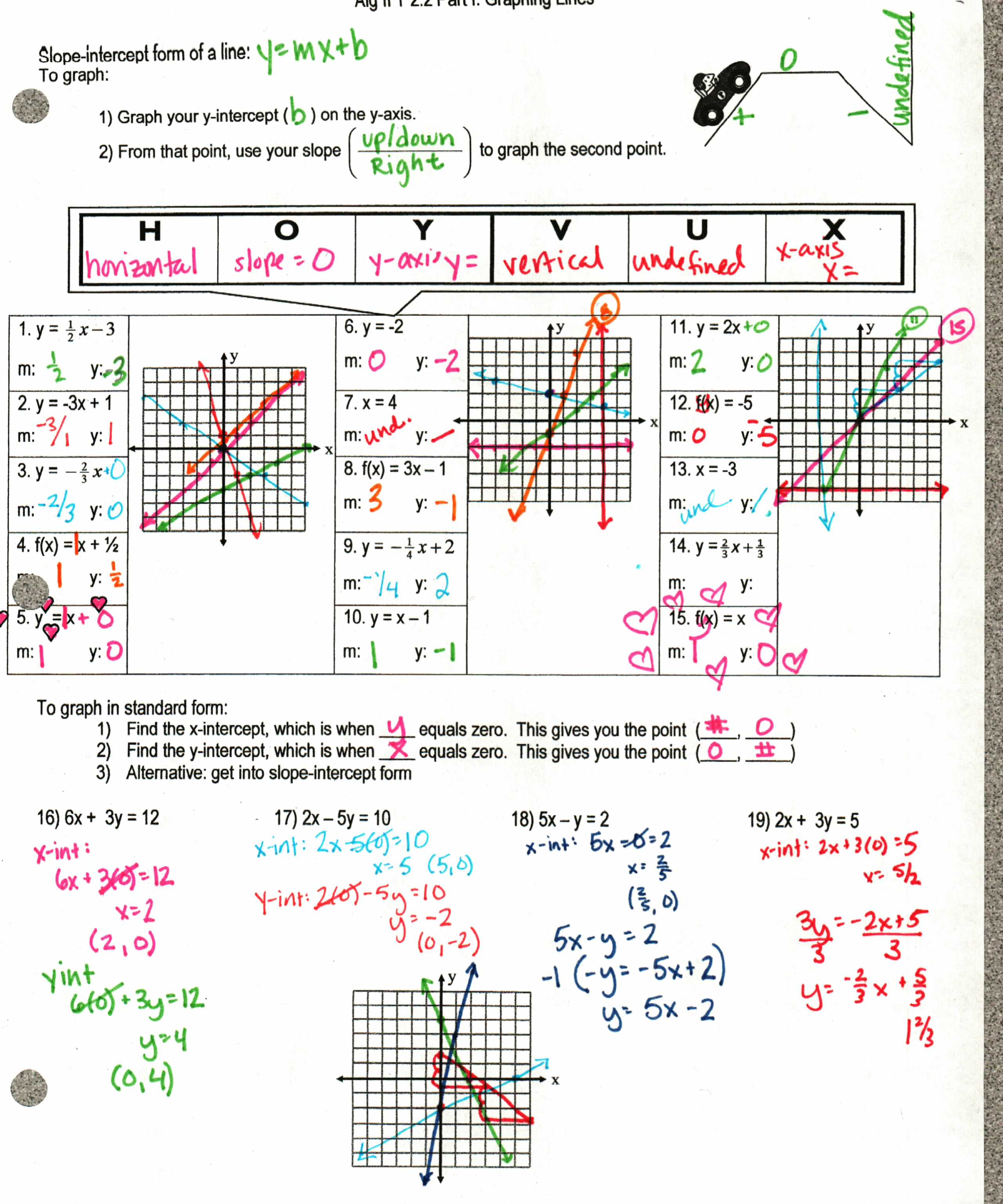File here. I used HOYVUX this year, but not sure if it’s my favorite. I usually go with “x(or y) = #” means we cross the x(y)-axis at that number. Also, note the hearts around #5) y = x. I tell them it is my favorite graph of all time, the graph all others graphs originate from and aspire to. And because it’s my favorite, it will be on every single test until every single student gets it right, which usually means it is on at least 4 tests.
This year, instead of my normal writing equation notes, I did this Translating Lines discovery instead (yes, it’s very similar to the Precal one I shared because it’s awesome)
File here. Next year, I’m going to add some more practice like the first 11, but wait on parallel/perpendicular/two points until the next day to reinforce the “new” point-slope form (they all learned it as y – y1 = m(x – x1) instead of y = m(x – h) + k) and also work a little on getting it into slope-intercept and standard (since that is what a lot of standardized tests use).
However, even without that, most did well on the in-class practice:
Or maybe you’d like a scavenger hunt with graphing, functions, and equations in slope-intercept and standard form?
This is just the first 2 pages; it goes all the way to X and takes most of a period to finish.
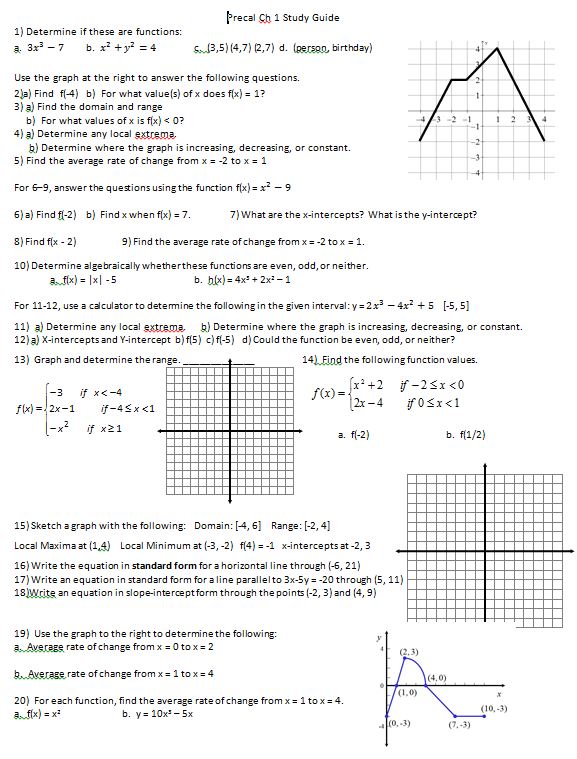
Or maybe you’d like to stop here and give a test? Well, here’s a study guide
Now let’s actually use these lines! Next year, I think I’d like to start with Mathalicious Domino Effect, or at least make that the first type of problem on the notes. Actually, I need to change a lot of the problems on here. I teach in a suburb, so my students have no idea about the ride fare of a taxi. Also, don’t set yourself up to talk about “expanding rods” in high school. And look how quaint #4 is–a toll phone call!
If you look below, I did take someone’s (??) suggestion about the new way of finding slope with a table and labeling the slope. Also note the mad-libs portion of the worksheet describing what the slope and y-intercept tell us, an idea I got from Mimi (@untilnextstop) (side note: I miss regular posts from Mimi! If you haven’t read her entire blog, you are missing out on some AWESOME activities and teaching ideas. I’d say I get at least 1/3 of my ideas from her. Also, she lives the most adventurous life!)
Then we did some linear regressions on the calculator (of course you could also use desmos), again practicing some “Math-Libs” on what part of the equation tells us. Note: next year, I need to add a negative correlation example.
File here. I must say I like the two part version of #5, where we find more data = more accurate (or at least a better picture). Which always reminds me of this xkcd comic:
This year I did Mathalicious Reel Deal (members only), which talked about movie length over the years. It didn’t go as well as I had hoped; there was a lot of handholding throughout and little “oh, I get it now!” moments. Maybe because it was the first time I’d done a Mathalicious lesson?
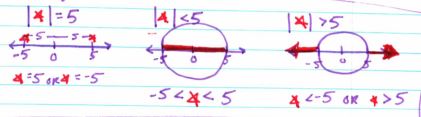
Then it was time for some absolute value, a discovery lesson that actually went well!
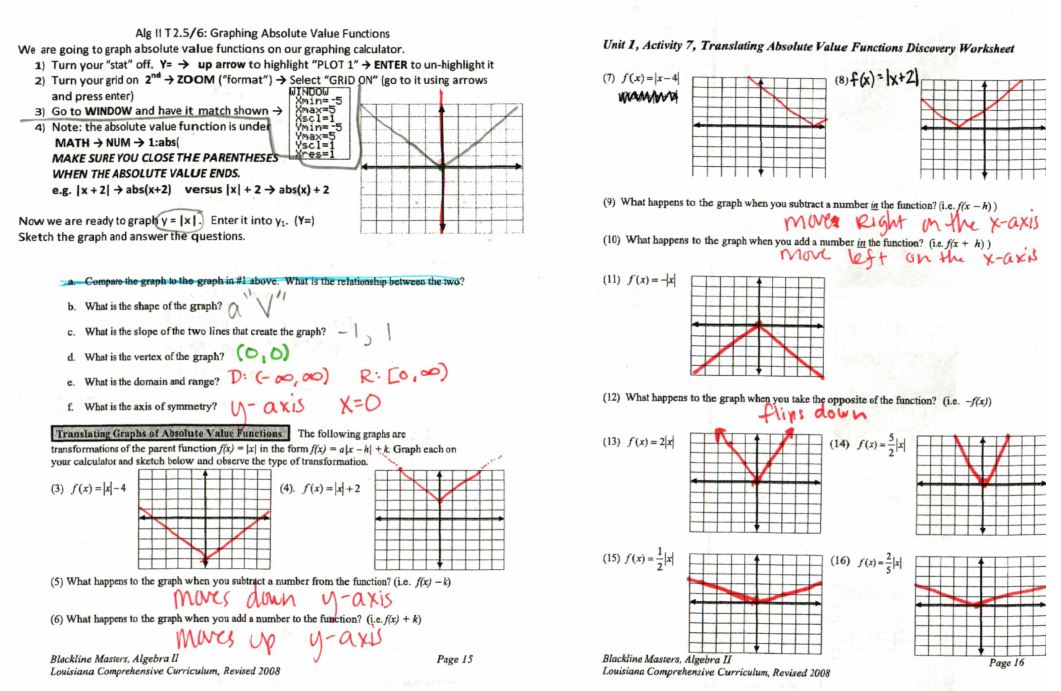
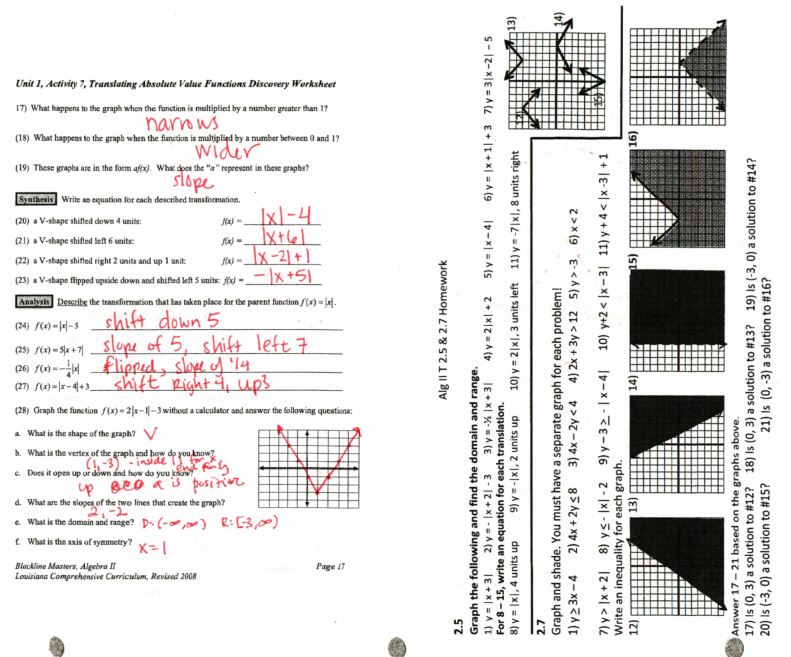I typed up the first part of the first sheet, file here. It looks like the rest came from the Louisiana Comprehensive Curriculum, the pdf file is here. The homework file is here.
Alternatively, if you’d just like some notes:
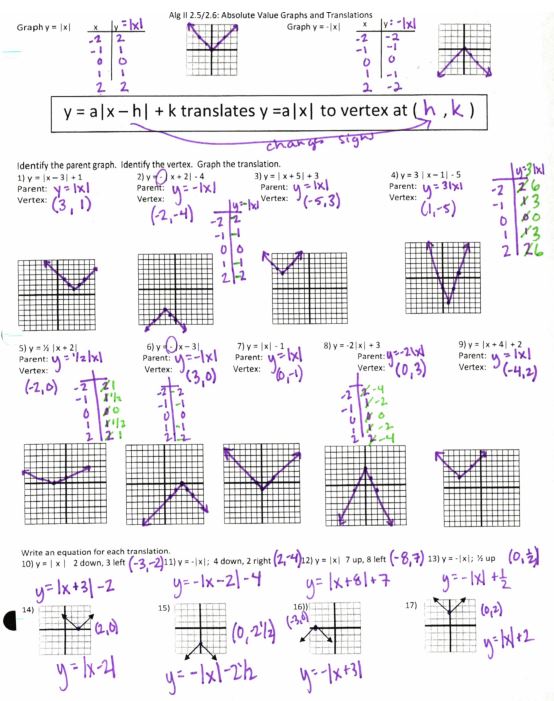File here. Also, check out that nice vertical stretch work on #4. I’d almost like them to do the chart and change the y-values instead of thinking of it as slope, since that won’t work for any other function. But the discovery activity was also really nice…hmmm….decisions, decisions.
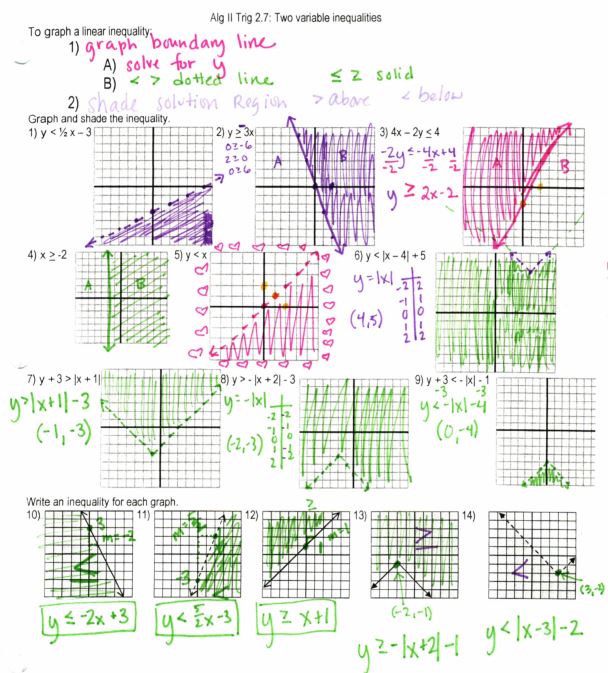
Well, at least I know how I like to teach graphing inequalities:
Hey, look, it’s my favorite graph again!
File here. (The shading on the last row usually prints nicely from the printer–I think it was a copy of a copy that I was using, so you couldn’t see it very well.) Also, no, we don’t have time for test points, we just go above and below. Hint: make them put their pencil on the line and then move it above (or below). That seems to help for when they secretly want to go left/right.
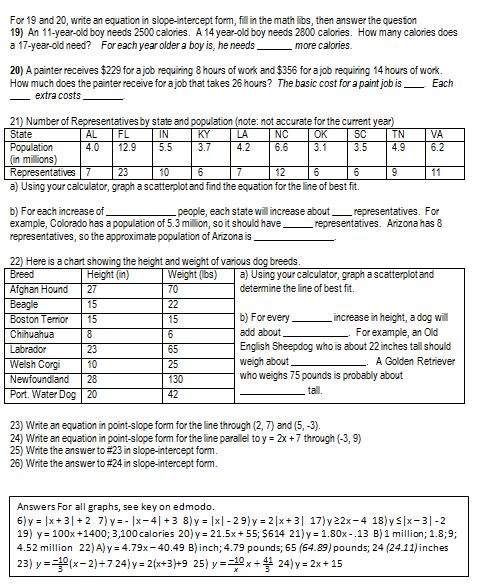
And finally it’s a study guide!
File here (print it out on legal, then copy two-sided and cut in half).
My thing
Ok, this is going to seem like a weird thing, but have y’all tried the Command adhesive shower products? 
They are seriously awesome. I hate the suction cup caddies that either (a) slowly slide down the wall or (b) quickly crash to floor (usually in the middle of night). We’ve had these in our shower for almost two years now and they haven’t slipped a bit! So treat your shower to a makeover this summer and install some of these. You can thank me later when you’re not woken up in terror at the sound of a burglar shower caddy falling.
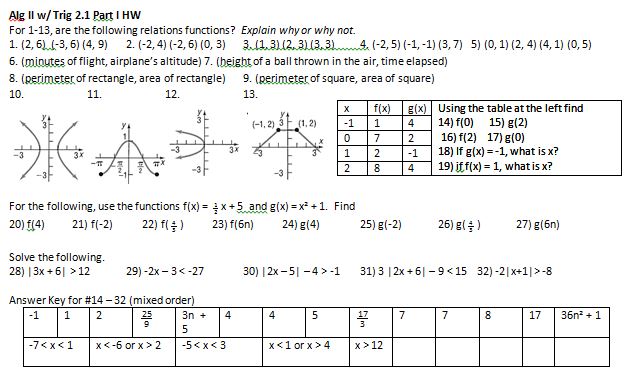
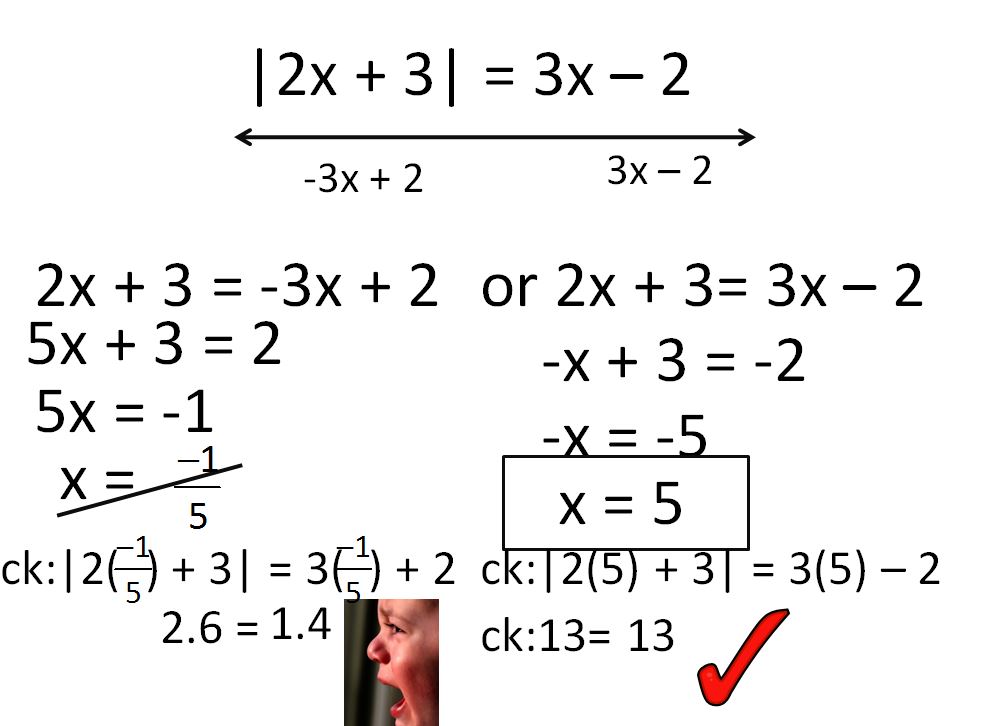
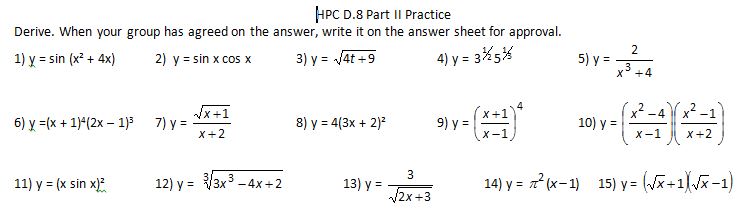
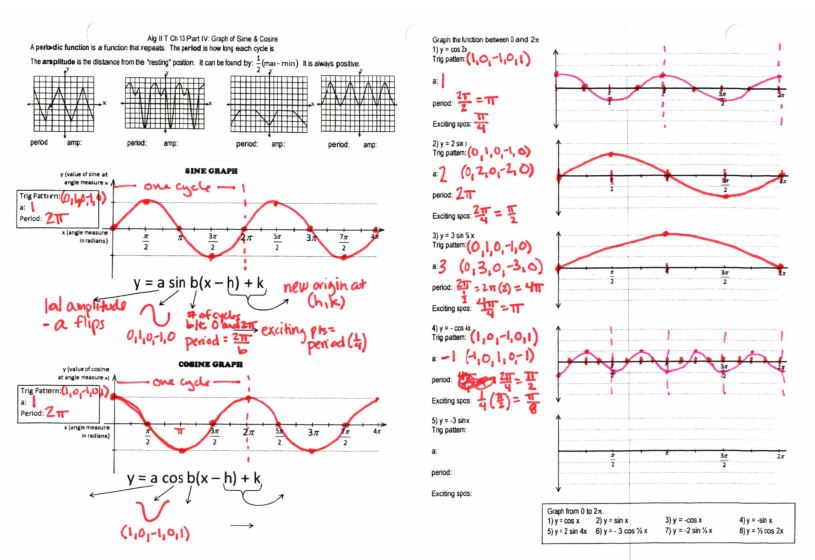
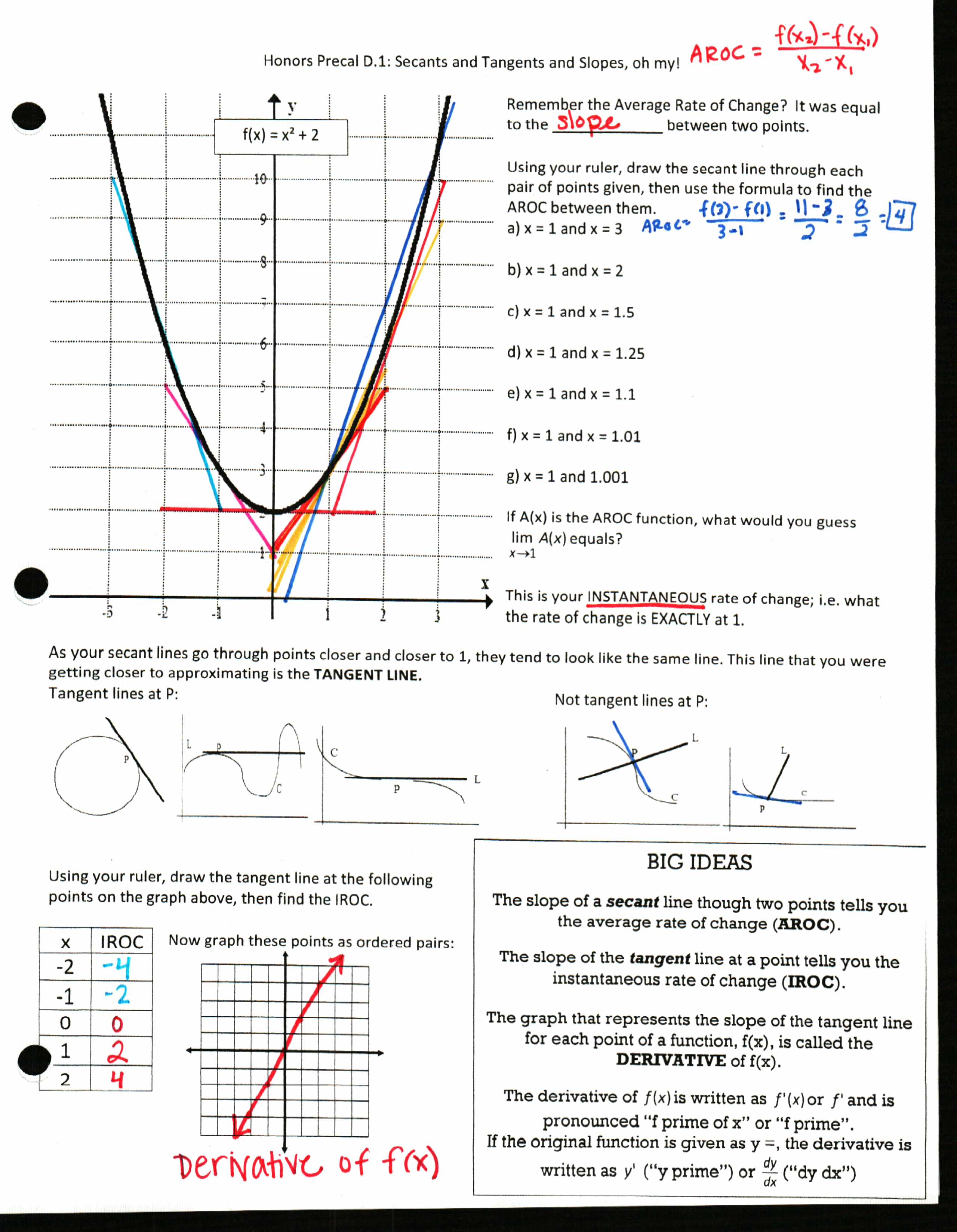
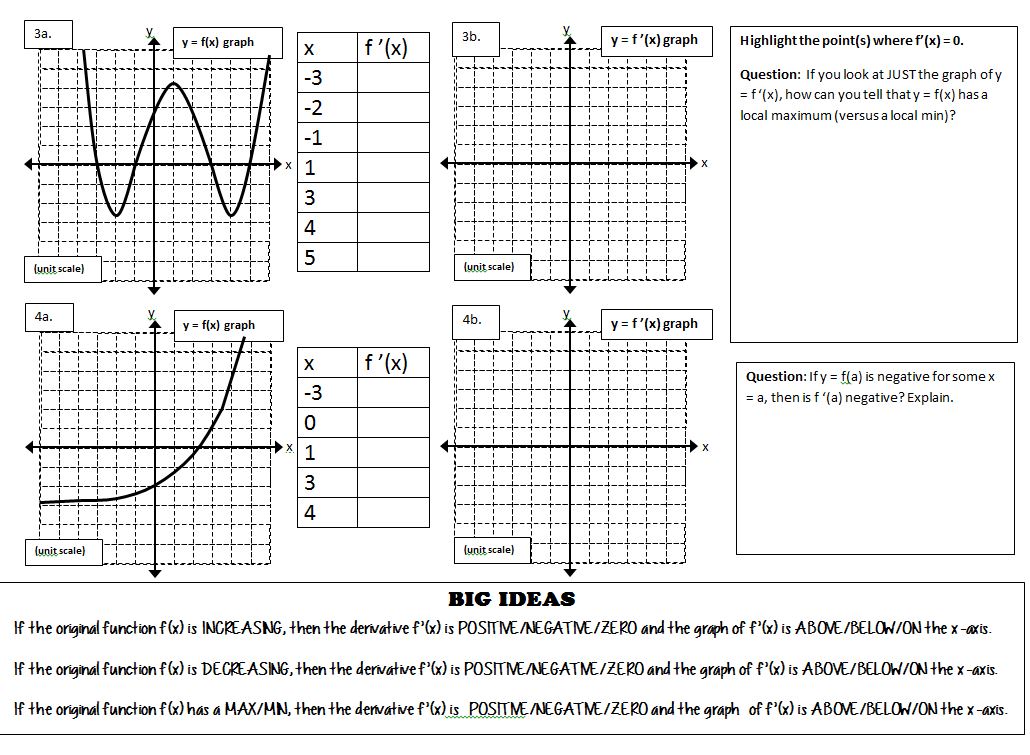
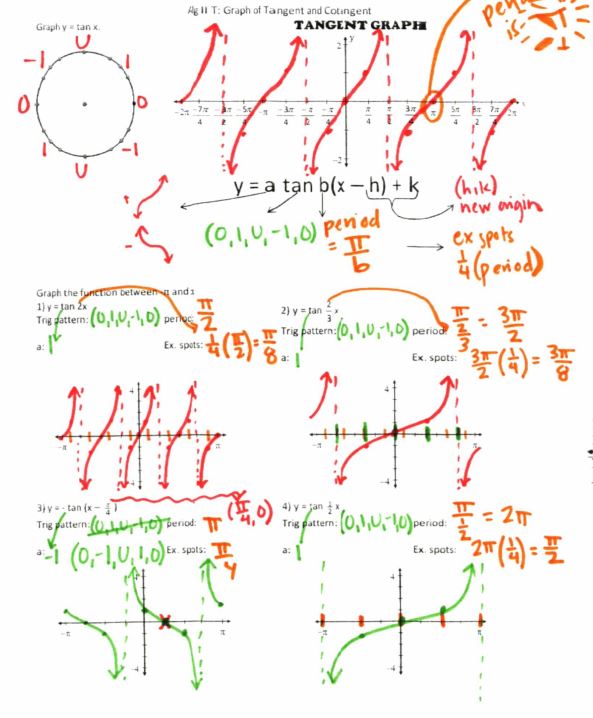File link.
