(See Part I for Intro to Derivatives.)
Ah, that fun day in Precal (or Cal) where you get to tell your kids all that work with the f(x+h) is about to be forgotten. Depending on time and interest, we talk some about patterns they’ve noticed so far, then we formalize it:
File here. And some homework.
If you notice, we also throw sine and cosine in there as an added bonus (plus it makes the chain rule more exciting in few days). The next day I like to do this practice from MathTeacherMambo (but I can’t find the original post for it). before we jump in product/quotient rule so they can get really good at the problems like the ones at the bottom before they try to solve all of them with the quotient rule. Because of time, we couldn’t do that this year and just did some derivative applications instead (which I just pulled from the textbook and are too boring to share).
But in Perfect World School (or at least a couple years ago), we went on to product rule and quotient rule. I showed them how we derive (pun intended) the rules and I remember last year, one student came in late and another told him, “You just missed the most mindblowing thing EVER!”
Also, check out that Color With A Purpose. I found the boxes really helped to see if you needed the product/quotient rule at all–each box must have a variable! For non-example, in #3, there are no boxes on 2 sin t because 2 doesn’t have a t, so no product rule on that part.

More boxes, and also more reinforcement of STOP DOING THE QUOTIENT RULE EVERY SINGLE TIME YOU SEE A FRACTION. SRSLY.
We also did some quotient practice from (guess who?) MathTeacherMambo. (Holy cow, how did I have all this time last year and NONE this year??)
Then the chain rule:

More boxing/Color With A Purpose. This time to see if we actually have a function inside a function.
File here.
Also, because it got cut off in my scan:
Then let’s throw it all together:
and practice it:
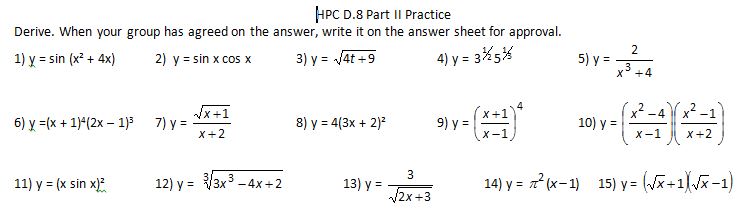
The “answer sheet” was a grid with 15 boxes on it. Nowadays, I would have them use group whiteboards/vertical non-permanent surfaces.
And because I like you, here’s the study guide for Part II of Derivatives (with bonus flashback to determining things from a derivative graph).
Next time, I’d like to spend more time on *good* application problems…like optimizing volume or maybe talk about when to enter the water to fetch a ball…WAIT WHY IS THIS A MAYBE?? OBVIOUSLY I NEED TO BRING ADDISON TO SCHOOL:
My Thing:
Just in time for wasting summer days, my thing this week is the game 1010! (I’ve already seen students play it, so maybe I’m behind the curve?) Were you a fan of Tetris? This is very similar, except they give you 3 pieces at a time and they don’t fall. It’s the perfect airport game if you’ve already completed Game About Squares.
What’s your favorite time wasting game? And what’s your favorite, “hey guys, wait til you see what math came up with to save you guys HOURS of time?!?” moment?




