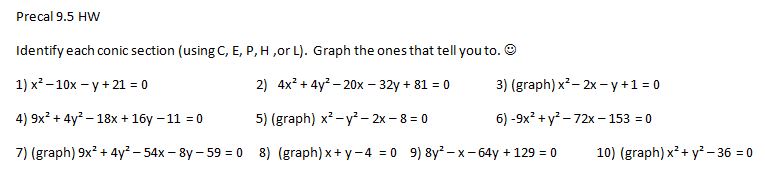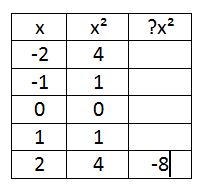tl;dr: What should one do if, after a week of lessons, a majority of your students are still struggling on a concept that you’re not even sure is all that important?
This week was a really rough week in Algebra II. My goal was to have them be able to graph a parabola given in 3 different forms, then at the end of the week, also show how we can use completing the square to transform standard into vertex form, maybe do some applications of quadratics as well. This is what happened:
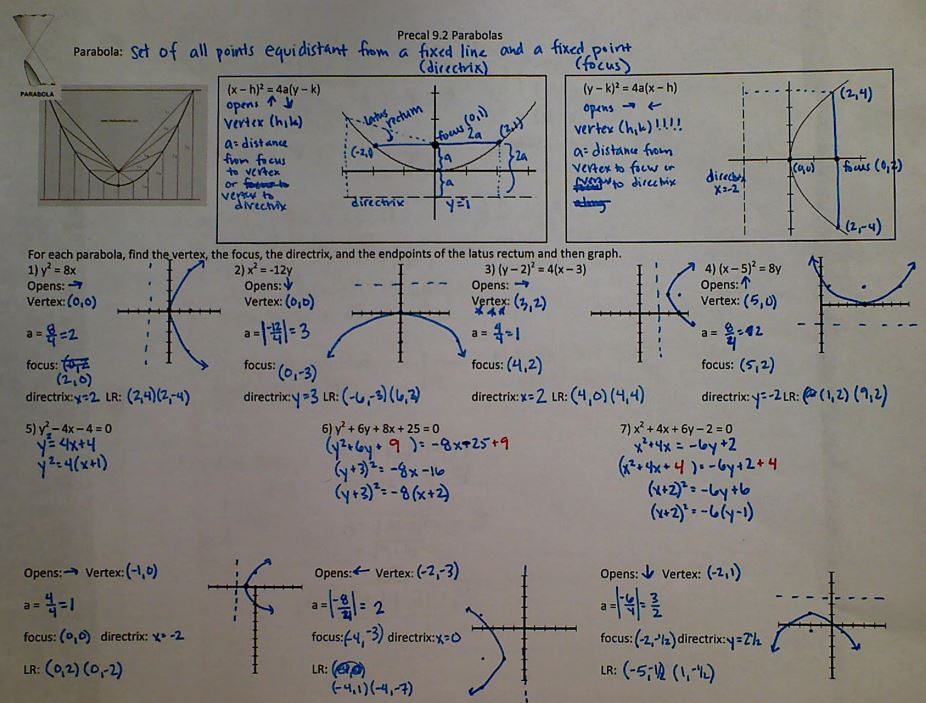
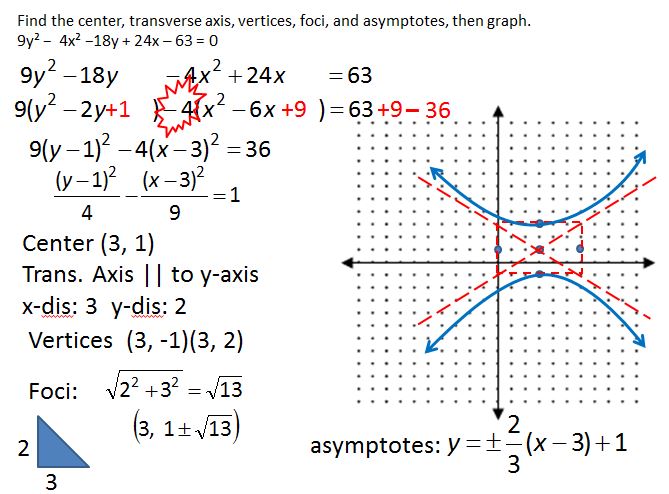
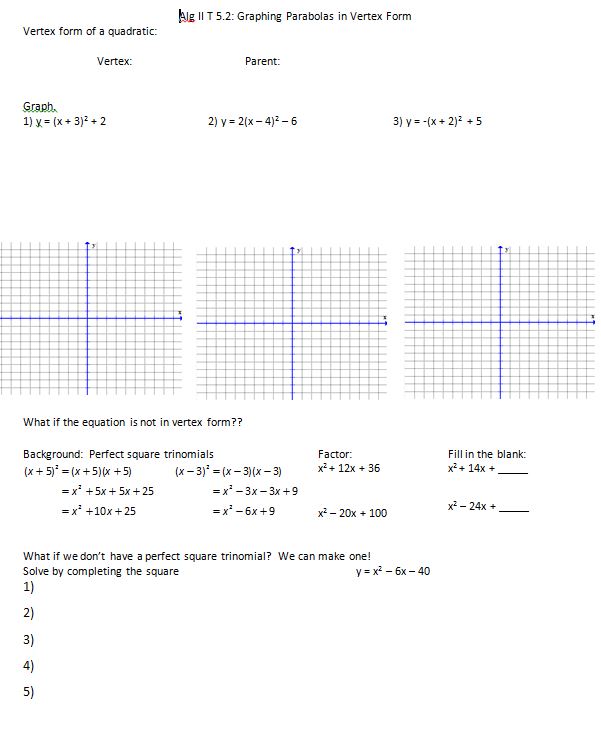
Day one: I want to update the chart I used last year, so I made this NTM:
(here’s the file, although after reading this post you probably won’t want it!) Ok, so this took us the entire class period. And it was horrible.
“hey guys, to find the y-intercept, what do we know about a point on the y-axis?”
“….”
“ok, well, let’s think about this point on the y-axis, what would its coordinates be?”
one meek voice: “(0, 8)?”
“Yes! So what should the x-coordinate be?”
“0?”
“Yes! So if I know the x is zero, how could I find y?”
“0?”
“Ok, that’s our x, what should we do with that to find y?”
“…”
“Ok, if I give you any x value, how could we find the y-value?”
“….”
(barely containing my frustration at both the students for not knowing and myself for being such a crap teacher that I haven’t even gotten this point across in the first semester of Alg II) “Well, we put it in for x. Because see how the equation equals y? This is how we can find any ordered pair if we know one of the coordinates! So plugging in zero for x in any equation always gives us our y-intercept!”
5 minutes later, for the next form:
“So, how would we find the y-intercept?”
“….”
I kid you not. Every. single. class. period. In retrospect, I think I should have had one example of each form under each category and worked through it, rather than just doing it as scratch work on the board. But I thought seeing it all together with the graph would make more sense. I was wrong.
Also, I thought this was going to be so easy that I might as well talk about where the graph is increasing/decreasing and positive/negative to fill in time. (Note: we had already done positive/negative when talking about quadratic inequalities). In case you didn’t know it already, talking about where a graph is increasing in terms of x and not y is one of the hardest concepts in math. Ask me how I know.
Day 2:
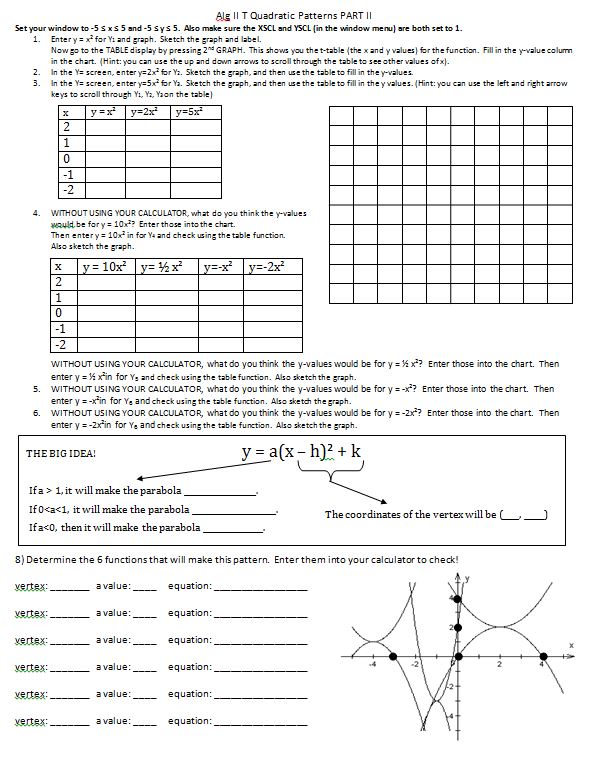
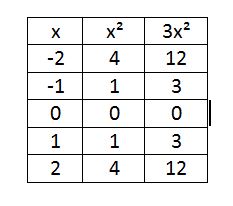
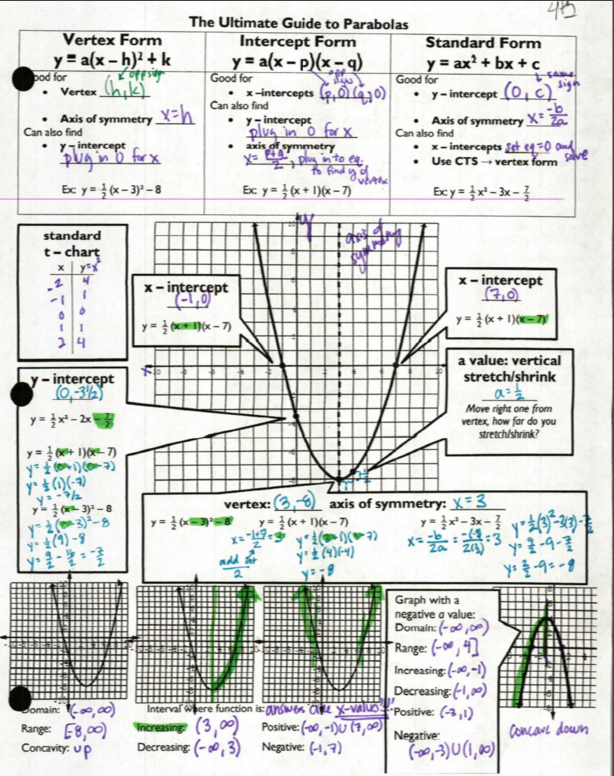
Onto the back (which I had planned to have finished yesterday! Ha!)
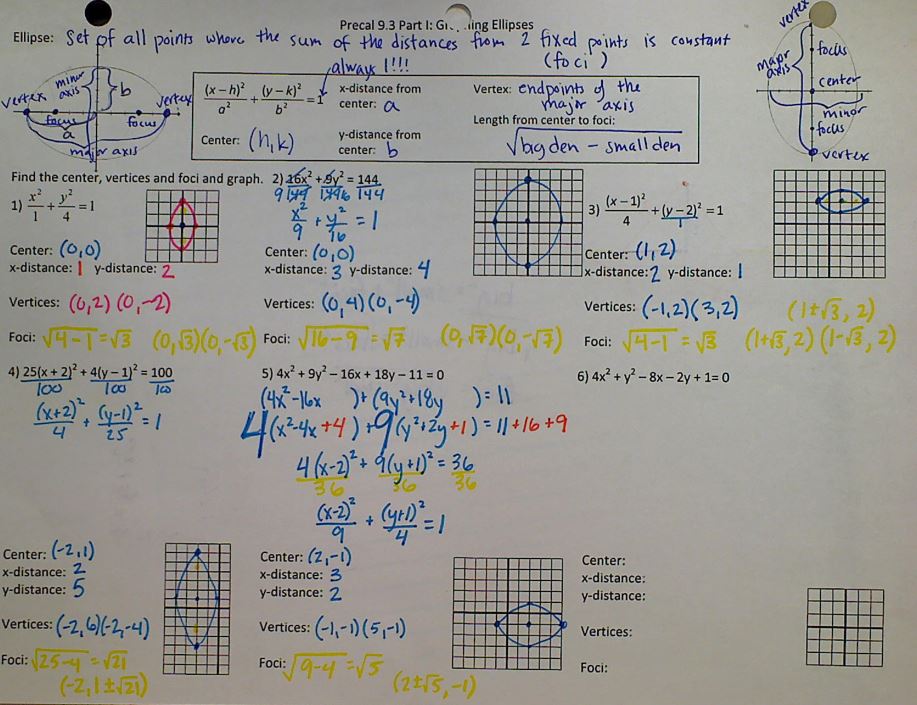
They were in partners and I let them work on each section for 3-5 minutes, then we talked about it. They were doing not horrible, but some didn’t know where to start. Again, in retrospect, I should have put “how to find the vertex” on the front, not “axis of symmetry” because they would tell me there were no instructions for the vertex. (I mean, yeah, except for the box at the bottom of the graph that had “vertex” and an example of each equation, but c’mon, that was all the way at the bottom.) We had about 7 minutes left at the end of class, just enough time for them to cut out their dominoes for tomorrow. The right side was homework. (The bottom was homework the previous night, because they didn’t do so hot on their unit circle test, either. So far this semester has not been off to a great start.)
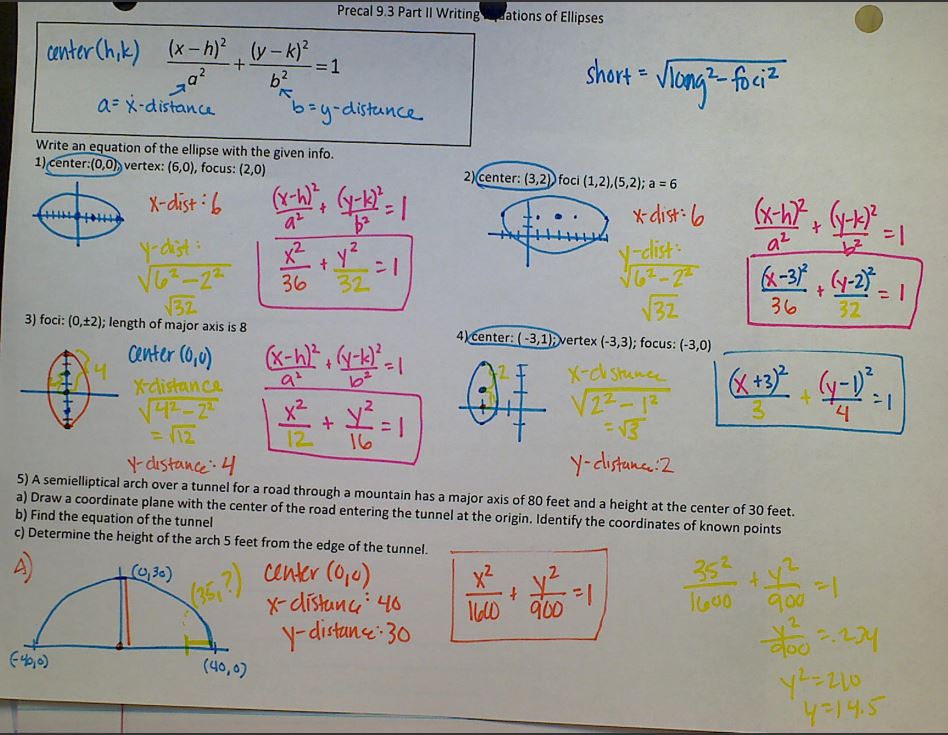
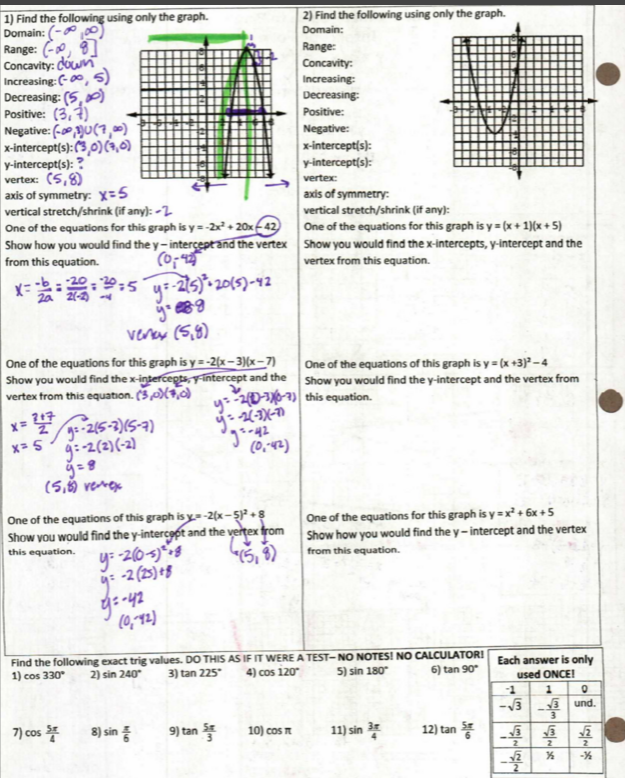
Day 3: Check homework; at least a quarter of them just wrote down the points under each equation instead of actually showing how we got them (like, you know, the example right next to it). Went through the homework problem and had them work with the Math Shell quadratic dominoes. Based on my previous experience, I had them cut out the graphs and match them to the equations (playing them as dominoes led to lots of silly looking-at-the-wrong-graph mistakes last year when we went to fill in the blanks). Then we rotated partners and checked. Then I revealed the correct answers and maybe 1/4 – 1/3 got them all correct, or had only one pair switched. Then I had them work on filling in the blanks. This seemed to go OK. At the end of the day, I gave them a worksheet that had three equations, asking them to find the important information and graph. In my extra long period, they had time to start on it and there was so much struggle. Like not even knowing where to begin. Like not even knowing that this was the same thing we had been doing for the last three days. Like this was the third day I just wanted to cry at the end of the period.
Day 4: “Ok, I think we maybe need to see the big picture of all these equations again.” So on the back of our worksheet, we did an example together of each of the three types. Then I set them loose on the front again. It was horrible. We have no idea what these numbers are. The x-intercepts are (-1, 0) and (4, 0)? That must mean the vertex is at (-1, 4)! Oh, the vertex is x = 5 and y = 3? Oh, that must mean the x-intercept is 5 and y-intercept is 3. Or the vertex is just x = 5. I went around putting out fires and got most of them through it, but I doubt they would be able to do it again on their own (ok, maybe 15% could).
So this bring us to where we are today: Not much farther in our knowledge of parabolas than we were on Tuesday, perhaps even less (or at least more confused). Also, may I remind you that this is Algebra II, so we’ve already seen these in Algebra I, and I have many, many, many more topics to cover this semester. These extra forms aren’t even in the course of study; I just thought it would be a nice review of parabolas by themselves (we’ve already had a whole chapter on transforming famous parent functions) and practice in seeing the same thing different ways and being able to see why some forms may be better than others.
My question is: do I throw in the towel?
I honestly think it would take at least two more days of practice for them to even be able to attempt a quiz on this. And what could I do differently during those two days that would help them improve? Other than, here is yet another example step-by-step. And I still want to cover completing the square and maybe some applications (as in, where is the ball at its maximum, how long in flight, etc…stuff they’ll see on tests and in other courses). Should I just say, this just wasn’t a good week of lessons. Let’s work on changing standard to vertex because we like vertex form and that’s the only type of graphing that will be on the quiz. Should I try the applications on Monday, which would give them more practice about finding y-intercepts, vertices, and x-intercepts? Should I just forget that last week happened entirely and start the polynomials chapter?
Any advice would be greatly appreciated. Leave it in the comments, or better yet, tweet me (@mathymeg07) so I can pick your brain even more.