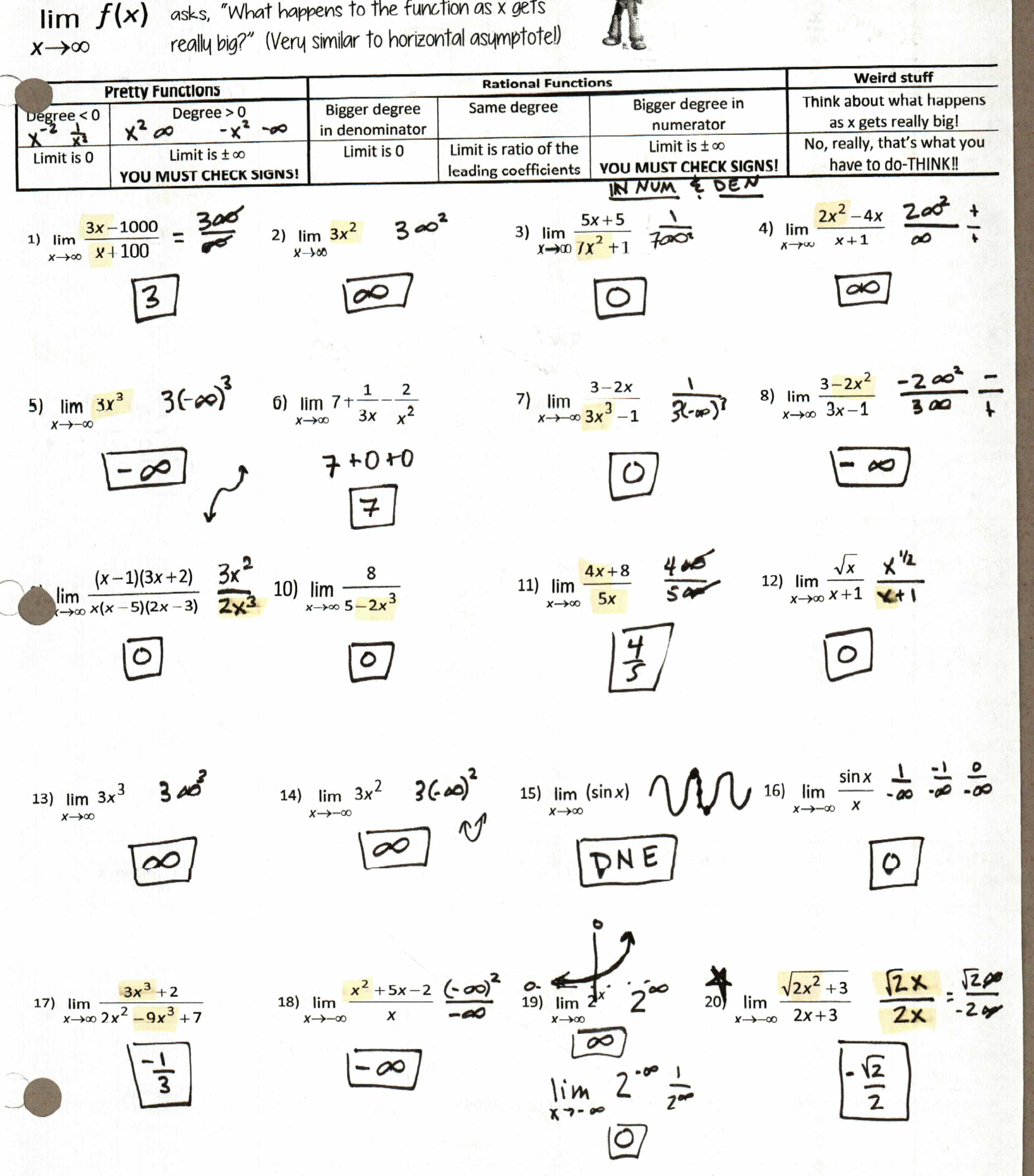
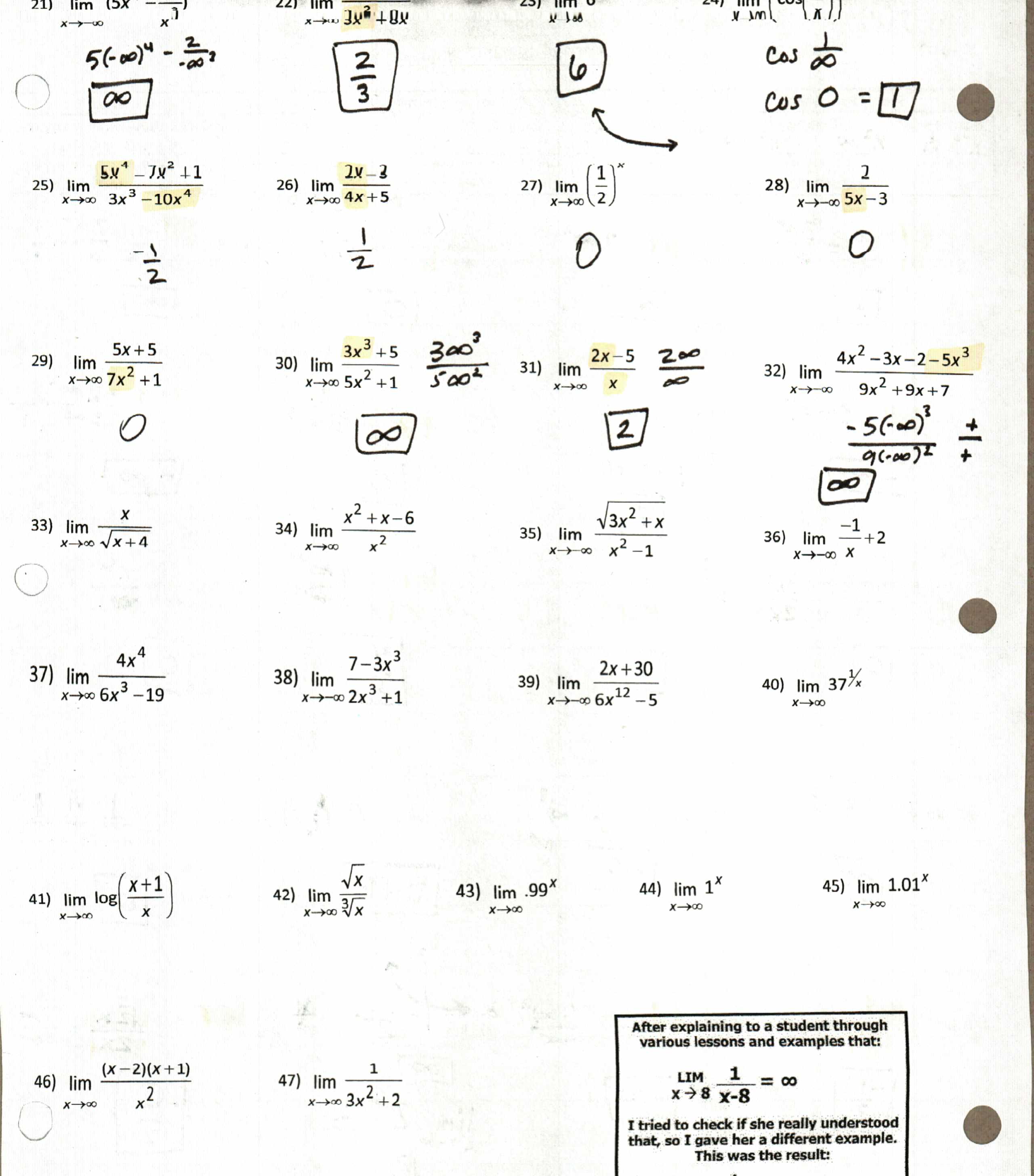
The reason you need this post is because Math Teacher Mambo has unlocked the secret to teaching radians so kids will understand. YES IT IS TRUE. She posted this fabulous idea on cutting out radian pieces to use, like this:
Image from mathteachermambo.blogspot.com
How can I describe using them in class? Well…
Exhibit A: After two days of working with both, I informally polled all three classes about whether they prefer radians or degrees. At least 25 – 50% raised their hands for radians, and many of them said it didn’t matter to them. That’s right, a class where kids prefer or at least do not actively dislike radians.
Exhibit B: In one of my classes, after the poll, I told them I was so excited because this was a new way of teaching it and it actually worked. One of the students asked, “so how in the world did you teach it before?” “We just thought about it.” Their reaction:
Exhibit C: After that reaction, another student said that they were great to start with, but then after a while they didn’t even need them. Woohoo!
Since I use NoteTakerMakers® instead of INB, I modified my NTM from last year to accommodate Shireen’s circle files:
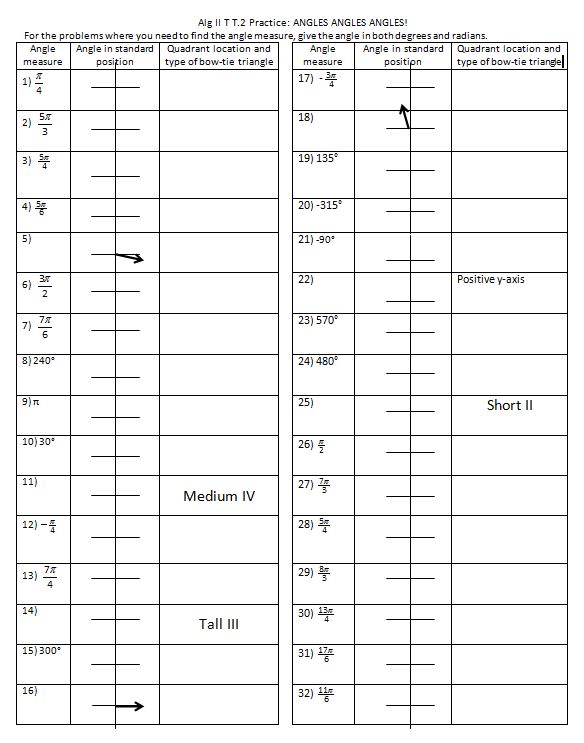
.doc fileWe started with degrees. By “bow-tie triangle” I mean reference angle (we had done trig values at a point the day before and practiced drawing our bowtie) and by “type” I tell them short, medium, or tall. We did the first five together and then I sent them on their way. Yes, with greater than 360 and negative angles, which was great because everyone had a different way of thinking about where they were.
Ok, just so I’m not kicked out of the #MTBoS, I would love to do a radians activity where we discover what they are, and that one radian is the same for every circle, and it takes 2pi of them to go around, lalala discovery learning, but I have 13 class periods to go from 0 to translating sine and cosine graphs, so I showed them a quick animation from Sam and pi, 2pi, pi/2 and 3pi/2 using Math Teacher Mambo’s empinadas analogy. (except with quesadillas because our Moe’s actually asks if you want them cut in half or fourths). We had just enough time at the end of class to cut out radians out, label them, and put them in a pocket (hint: Give each student a third of a piece of paper. Fold strip into thirds. Tape two sides and you got a pocket with flap. You can even tape it down to the NTM between the two circles, but it does over lap the chart a bit. I could probably make it pretty so it doesn’t, but I didn’t.)
The next day we talked about the radian examples at the bottom of the NTM. After the examples I asked them about what type of triangle we will have with denominator 6, 4, 3, and 2. I think next year, I’ll have them cut out the pieces like this:
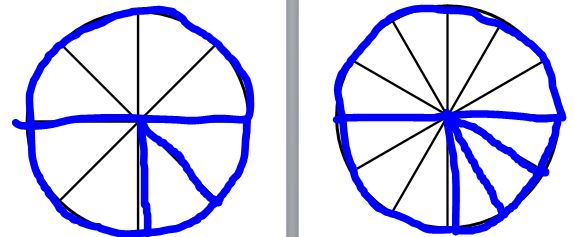Because lining up 7 or 11(!) of the wedges was time consuming and easy to land on the wrong space. Plus hopefully this might help them think, “is this more than a whole quesadila?” when they are deciding which pieces to use.
After the examples, I let them loose on this page:
I stamped the first five and ten as they were working to make sure they were on the right track. They didn’t even balk at the last few that were greater than 2pi!
Warning: the rest of the post is less essential than those radian cut-outs. 🙂
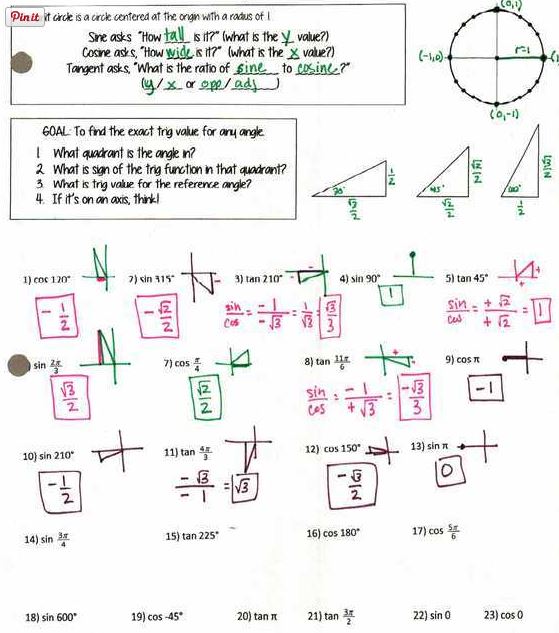
The next day was the big intro to the unit circle. I’ve moved away from “these are the coordinates, let’s memorize the unit circle and draw it on everything really quickly” because I realized when I started teaching precal we need to know sin 5pi/6 without having to draw the whole thing. So instead we talked about short/medium/tall triangles and just remembering 3 numbers: 1, 2, 3 and which one is short/medium/tall (or skinny/wide). I have them draw the triangle for each question. I think maybe I should also have them highlight the part we care about? Or now I’m thinking (and I’m going to try this tomorrow with reciprocal functions) of sacrificing one of our wedges and making it a triangle we can label and move around. I’ll report back.
Doc file and extra practice file
We spent the next day practicing and me stamping off correct answers, which I need to find an equitable way to do. I normally go around the room and stamp, but I always seem to miss tables. I need one of those numbered ticket things like at the butcher or Joann’s. Anyone have any great ideas on that?
They are definitely not where I want them to be after 5 days of this, but I think they are getting there. We shall see. Maybe I’ll just throw in the towel and start doing timed unit circle quizzes again.
