We finished up our limits chapter and the test results were….underwhelming? There were no HORRIBLE grades (not even a lot of F’s) but there were only a few outstanding grades. On the other hand, the majority of them did great with graphical limits and algebraic limits except for one-sided limits approaching an asymptote. Which, in retrospect, I may take out doing algebraically next year (or at least if I teach regular precal). I mean, we end up just making a mini-graph anyway, so why not just keep it in the graphing section? And at least no one gave this as answer:

Dude, that may be my favorite math equation pun, right after (sin x) / n = 6.
Also, the ant analogy (see my last limits post) worked a bit too well. At least 10 students “explained” that the limit was equal to the y-value of a hole “because the ants can still reach across” or “the ants will still be at the same place.” So if you’re an AP reader next year and see a lot of talk about ants, you’ll know why.
Here’s what the last half of the chapter looked like:
1) I redid the piecewise function worksheet to have more exciting piecewise functions. This took them the better part of a 47-minute period. File here.
 I have to admit I feel like I must not be doing my best as a math teacher when at least three students ask me “since 2x +10 doesn’t fit on the graph, can I graph x + 5 instead?”
I have to admit I feel like I must not be doing my best as a math teacher when at least three students ask me “since 2x +10 doesn’t fit on the graph, can I graph x + 5 instead?”
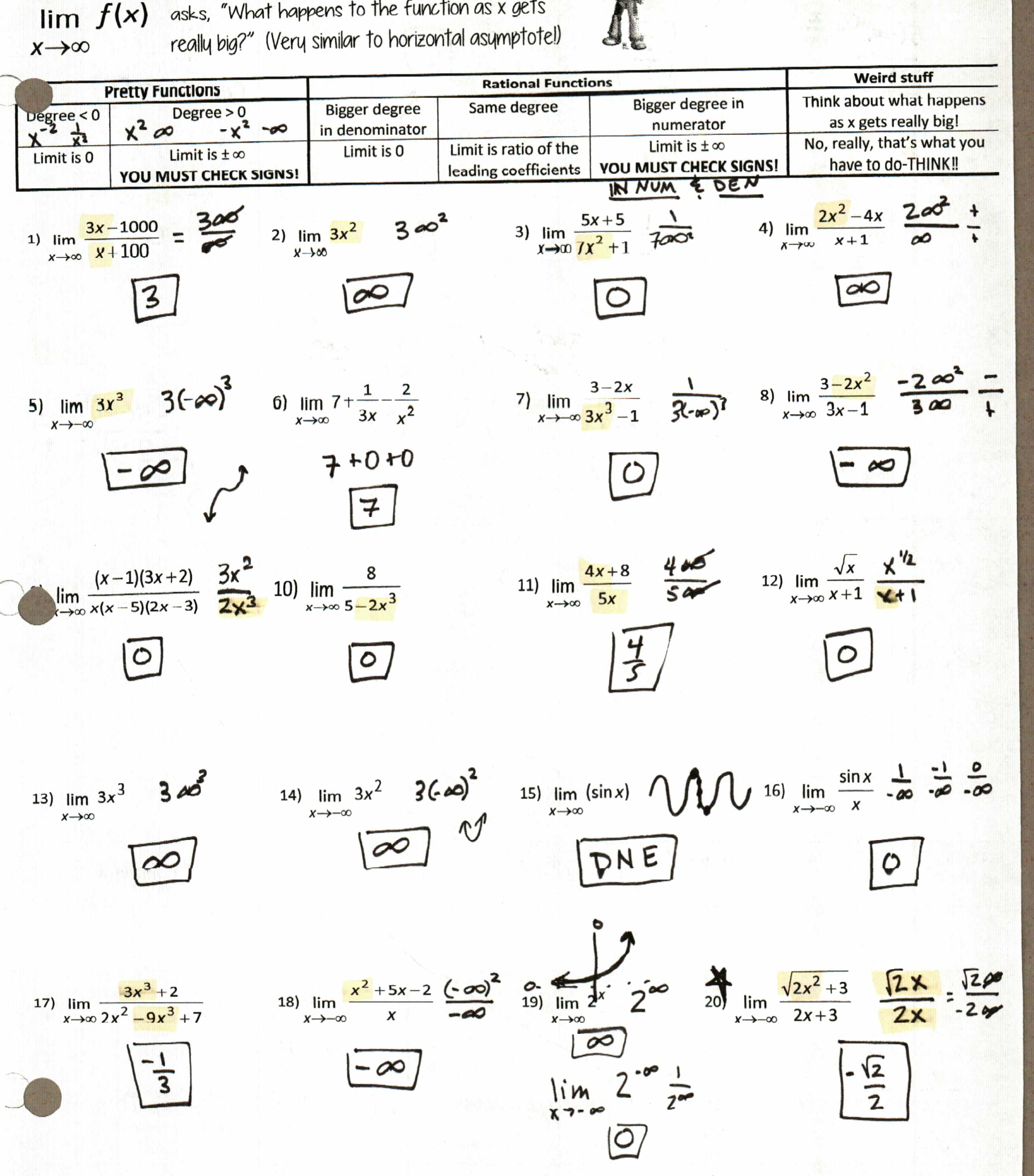
2) Then we jumped into finding limits algebraically, with a chart that I think is fabulous (but I may be biased). File here, and some homework just cause I like you.
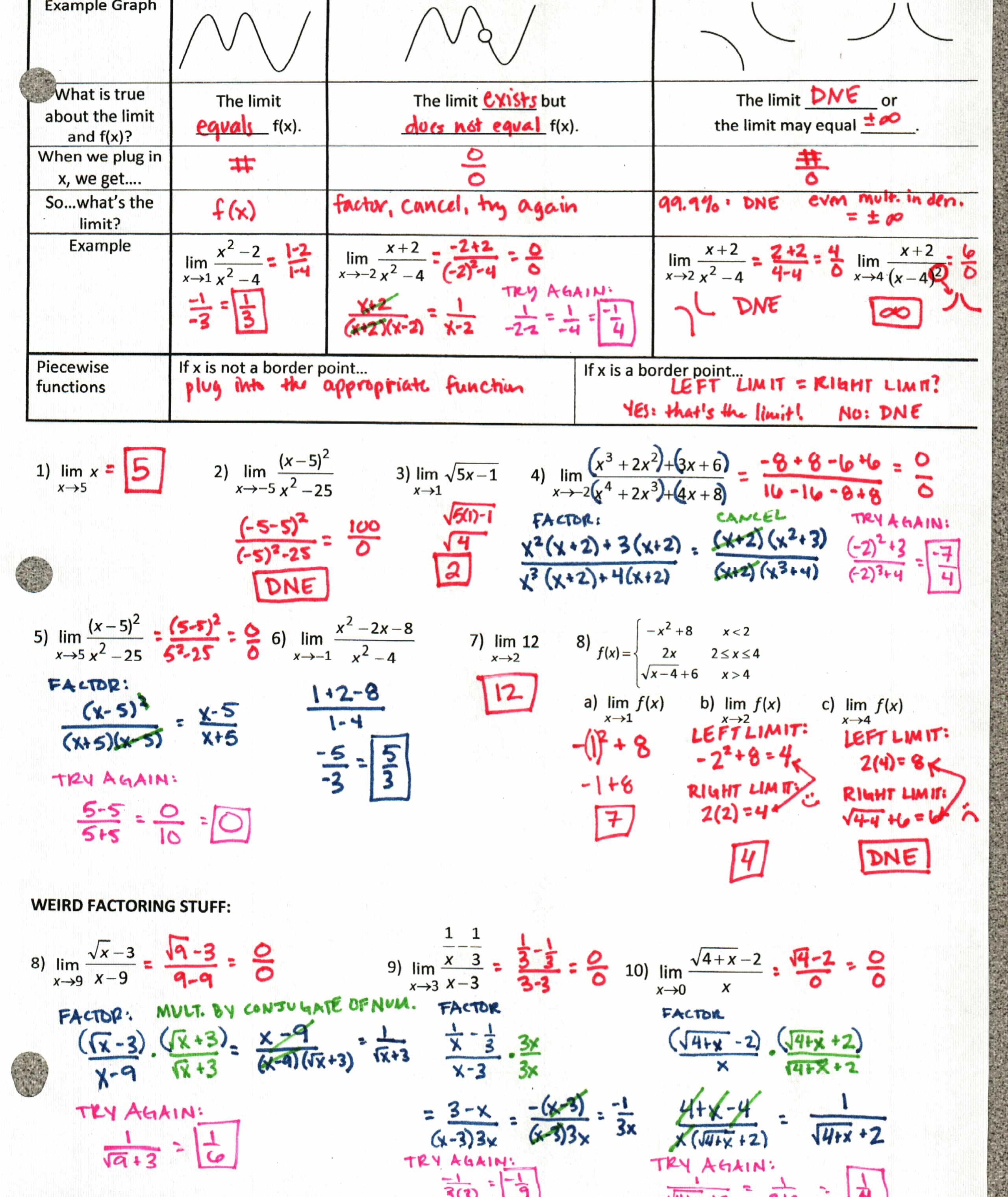 (also, check out that amazing multiply-by-the-common-small-denominator action happening in #9).
(also, check out that amazing multiply-by-the-common-small-denominator action happening in #9).
3) I’m continually amazed at the fact that no matter how often I told them you need to SHOW me algebraically all three rules when I ask about continuity, I still had maybe 5 that were like, “yep, looks good to me; you can draw it without picking up your pencil!” Here’s the file and some homework. Yes, the last two on the homework end up being beginning-of-the-next-class-period discussion questions. Also, cut down the first part of the homework by half.
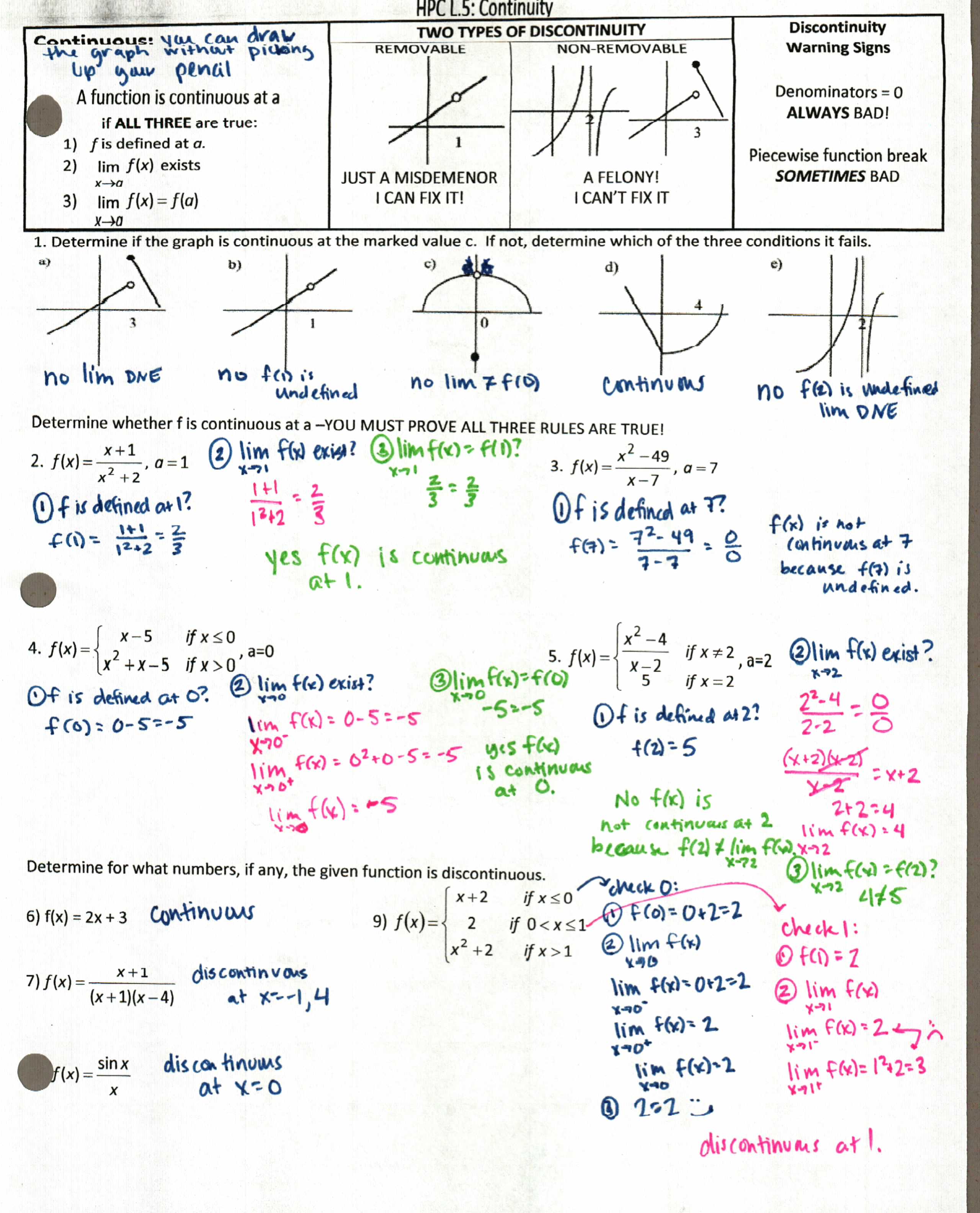 I also enjoy it when students put smiley or sad faces in the middle of problem because I do it.
I also enjoy it when students put smiley or sad faces in the middle of problem because I do it.
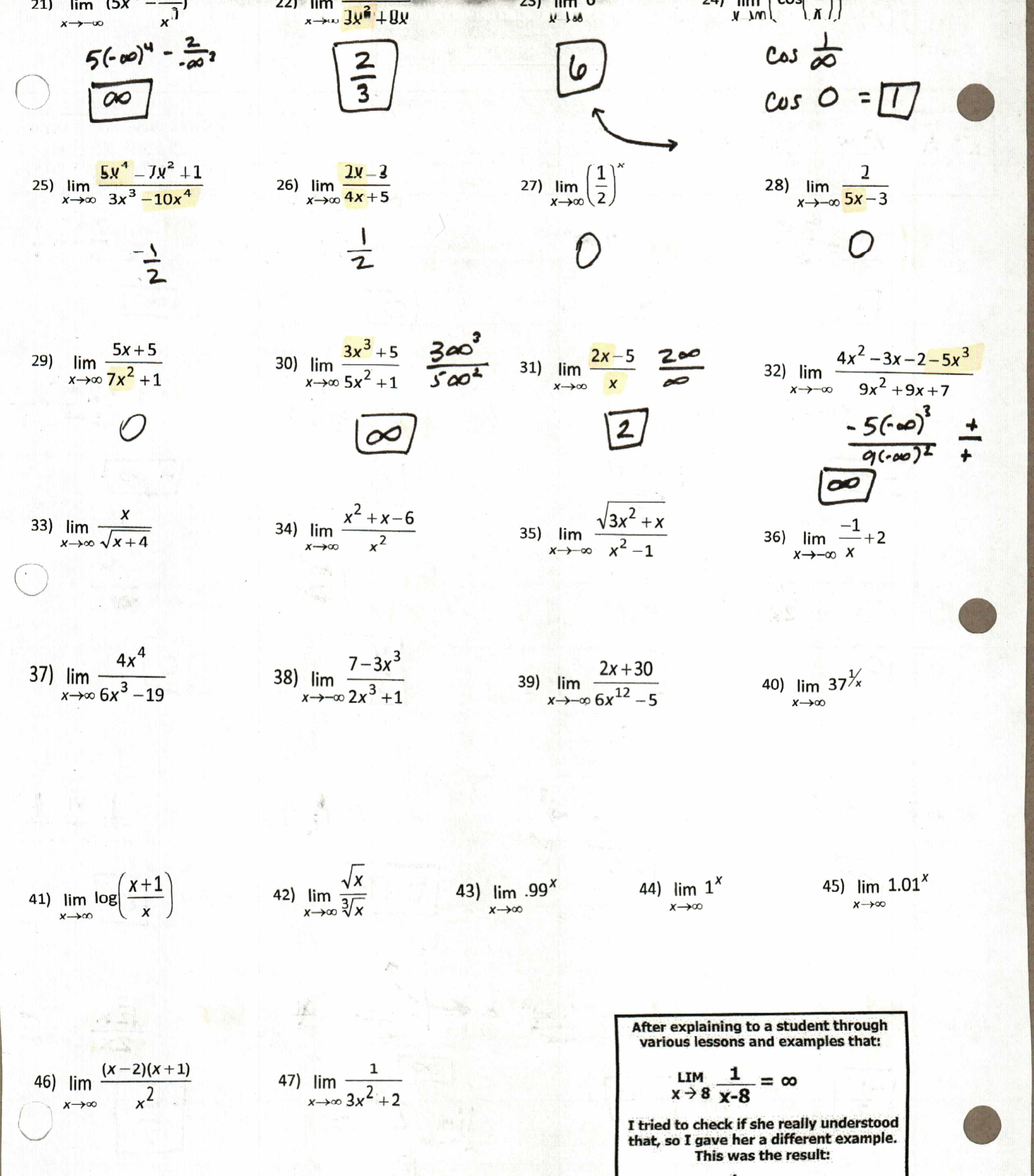
4) To Infinity….and BEYOND! (Aw, sorry you got cut off on my scan, Buzz). . I think highlighting the biggest power really helped. This is also the first year we “plugged in” infinity and I think that helped, too. And trust me, just omit #20. Save that sort of heartache for Calculus.
(file here)They finished the rest for homework. Be sure to talk about #43-45 the next day–how .02 difference affects the limit at infinity! Also, this was funny: a student was asking about #40 (37^(1/x)) on the way out of class. So I was writing on the board 1/∞ then she said that was 0, so I wrote 37^0. A kid from my next class walked in and said, so 1/∞ = 37 degrees? 🙂 I told them we should totally start using 37 degrees as our fallback answer for any question.
That was the last lesson before a couple of days of review. And just to make sure I’ve covered all limit jokes and puns:

Done.