Casey (@cmmteach) says, “MAKE ME A POSTER!” and I say, “HOW SPACEY?”
.pdf and .doc and yeah, because that would use a crapton of ink, bwpdf and bwdoc.
Then Julie (@jreulbach) says, “I NEED THAT IN A POSTER!” and I say, “I FEEL VAN GOGH IS SORT OF PICKY ABOUT USING HIS STUFF”
Then no one says “MAKE ME A POSTER OF THIS QUOTE, TOO!” but I think they just didn’t realize their classroom was incomplete without it so YOU’RE WELCOME, EVERYONE.
Updated: I also made a color version of the above poster: .pdf
Then Friday night on twitter we got into quite the discussion of (h, k) and function transformations, because that’s what cool kids do on Friday nights. Julie was lamenting at kids not sure what to do first…reflect, dilate, shift? So I mentioned what I call the S.S. method of graphing after one of the best math teachers with whom I’ve ever had the privilege to work. I’m not going to lie to you; I didn’t trust it for a while. But then after a couple of years (!) she finally convinced me and it is beauty and efficiency all at once. Then Julie says “GIVE ME AN EXAMPLE” and I say, “WELL HERE’S A WHOLE BLOG POST ABOUT IT ARE YOU HAPPY NOW?”
So you spend time talking about what the various parts do, maybe with some discovery desmos, or some crazy function match game with worksheet. (hint: don’t use the t-tables! it just confuses the issue!), or the beautiful HOLY COW SO THAT’S WHY f(2x) COMPRESSES activity (which yes, here’s a quick showme video because Elissa said “CAN ANYONE HELP?” and I said “I WILL SHOWME YOU” even though other tweeps answered her much better than I did).
After all of that, it finally gets down to the nitty gritty of graphing a real function with all sorts of exciting things happening. And yes, yes, you could do all the shifting and dilating and reflecting, and substituting (M, N), but then I don’t know how that would be any quicker than just plugging points into the original equations after all that work (don’t get me started on the people that have them draw a graph for EACH TRANSFORMATION like we’ve got all the time in the world) and the Cal teacher would like them to be quick and efficient at these graphs.
But the good news is I can multiply and divide really well and I’m also really good at counting from the origin. And that’s all that’s needed.
1) Mark (h, k) with a small x. This is your new origin.
2) Take your basic t-chart (-2 to 2 normally does it for me, unless there’s domain or excitement issues). Multiply/divide x’s/y’s as needed. Feel free to multiply/divide by negatives in the SAME STEP if a flip is involved because we are that CRAZY GOOD AT MATHING.
3) Graph your t-chart from your new origin. SHAZAAM. Feel free to label points counting from the original origin if your teacher’s into that sort of stuff.
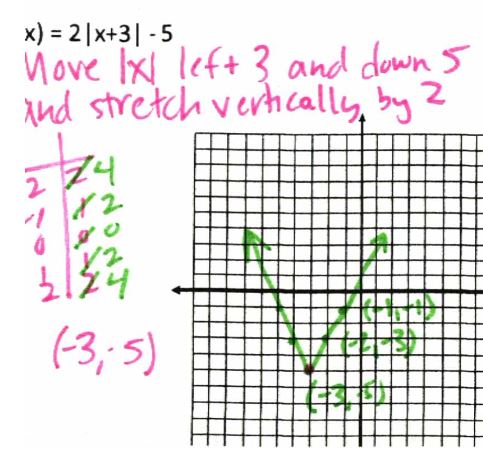
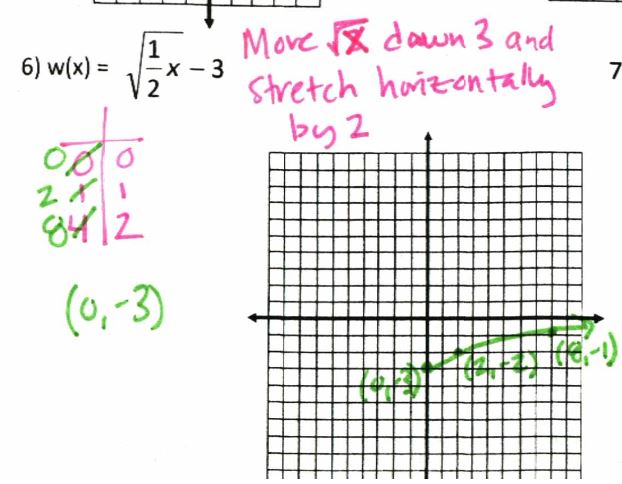
Here are some examples:
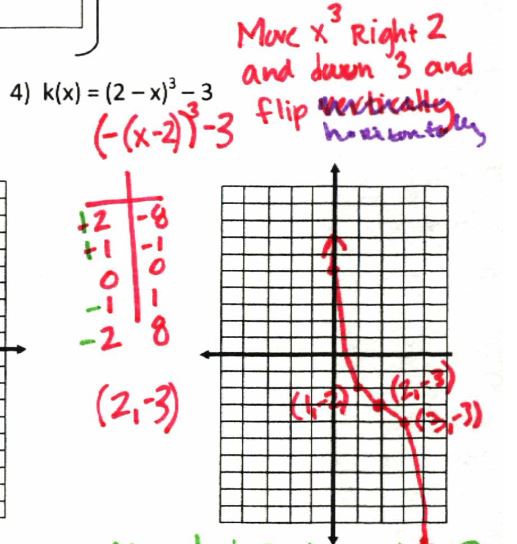
 The one catch–a negative INSIDE the function. We just have to do some reorganizing:
The one catch–a negative INSIDE the function. We just have to do some reorganizing:
(and some of us need to learn the difference between flipping horizontally and vertically. I know which way to flip; I just always call it the wrong thing. I’ve started going with “flip across x-axis” or “y-axis”).
Anyway, maybe this is what most of you do anyway? But I always have some teachers that are freaking AMAZED by it when I start graphing these babies at workshops so maybe you were, too. If you want more, here is the notetakermaker and the filled-in version.
Full disclosure: Of course y’all know Casey, Julie, and Elissa are three of the sweetest people on twitter and would never ask for things in the manner in which I implied. So I hope y’all consider this post just a feeble start to paying back all that MTBoS has done for me!