I’ve already blogged most of my matrix notes on this post (and as always, you can find all of my Algebra II Files and FAQs here), but I did do a new introduction to matrix multiplication that I liked:
(NTM file here, practice file here) Sure, you have to do a little teacher manipulation to make sure that the second matrix on the calzone example is a column matrix, but I think it really helps to see why we multiply matrices like we do, and what the resultant matrix tells us.
It also gives us a reason to play this in class:
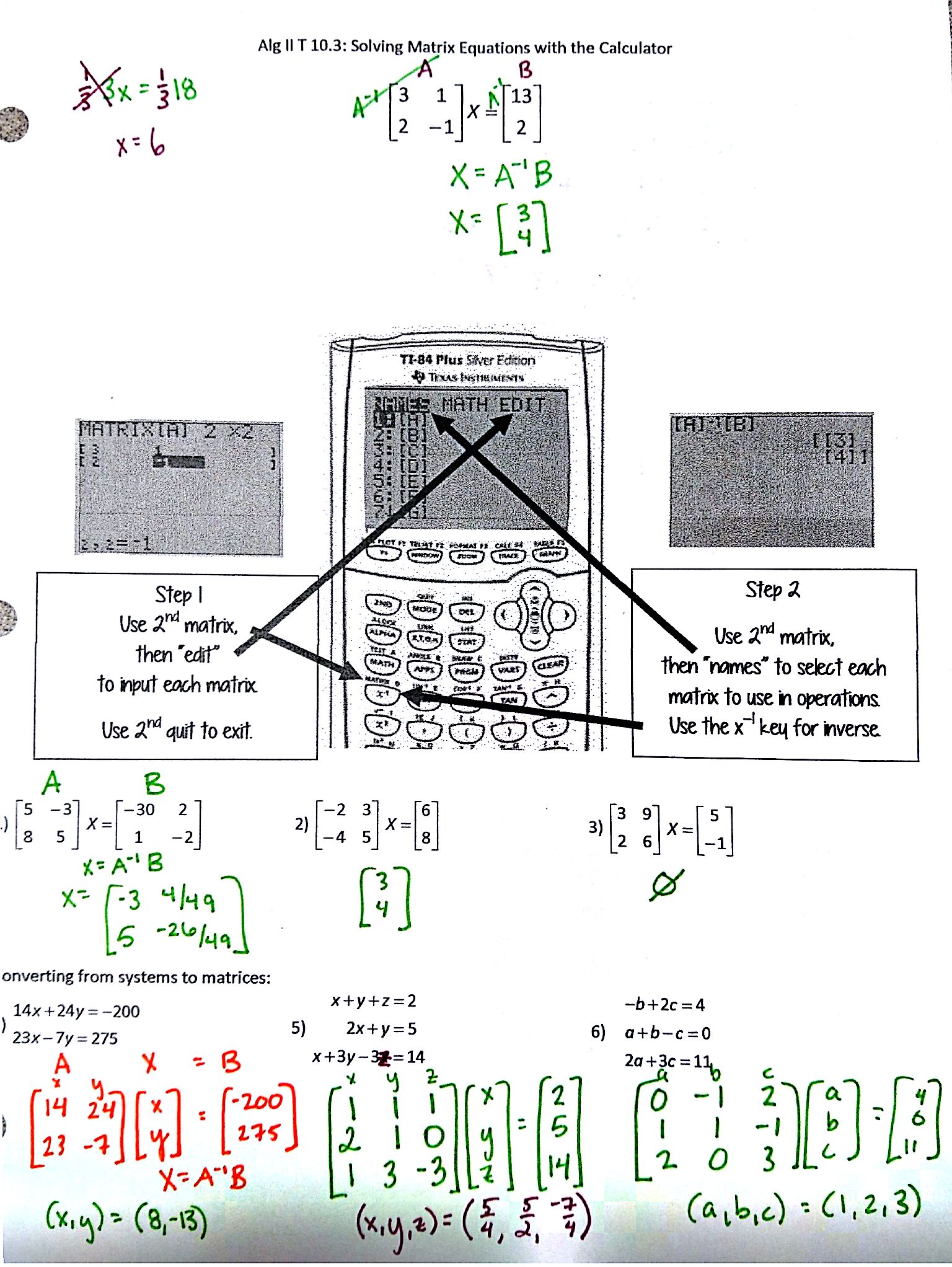
And as an added bonus, a pretty worksheet with a calculator picture and arrows! (Also I totally skipped finding determinants and inverse matrices by hand. Sorry, but sometimes you gotta ruthlessly cut stuff.)
(file here) Yes, it is required that you play Jackson 5 after the last problem. REQUIRED.