tl;dr: What should one do if, after a week of lessons, a majority of your students are still struggling on a concept that you’re not even sure is all that important?
This week was a really rough week in Algebra II. My goal was to have them be able to graph a parabola given in 3 different forms, then at the end of the week, also show how we can use completing the square to transform standard into vertex form, maybe do some applications of quadratics as well. This is what happened:
Day one: I want to update the chart I used last year, so I made this NTM:
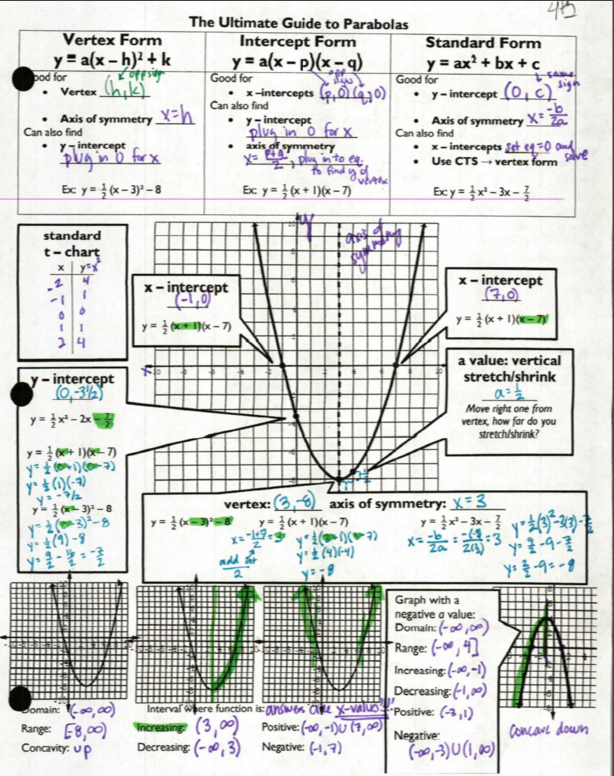
(here’s the file, although after reading this post you probably won’t want it!) Ok, so this took us the entire class period. And it was horrible.
“hey guys, to find the y-intercept, what do we know about a point on the y-axis?”
“….”
“ok, well, let’s think about this point on the y-axis, what would its coordinates be?”
one meek voice: “(0, 8)?”
“Yes! So what should the x-coordinate be?”
“0?”
“Yes! So if I know the x is zero, how could I find y?”
“0?”
“Ok, that’s our x, what should we do with that to find y?”
“…”
“Ok, if I give you any x value, how could we find the y-value?”
“….”
(barely containing my frustration at both the students for not knowing and myself for being such a crap teacher that I haven’t even gotten this point across in the first semester of Alg II) “Well, we put it in for x. Because see how the equation equals y? This is how we can find any ordered pair if we know one of the coordinates! So plugging in zero for x in any equation always gives us our y-intercept!”
5 minutes later, for the next form:
“So, how would we find the y-intercept?”
“….”
I kid you not. Every. single. class. period. In retrospect, I think I should have had one example of each form under each category and worked through it, rather than just doing it as scratch work on the board. But I thought seeing it all together with the graph would make more sense. I was wrong.
Also, I thought this was going to be so easy that I might as well talk about where the graph is increasing/decreasing and positive/negative to fill in time. (Note: we had already done positive/negative when talking about quadratic inequalities). In case you didn’t know it already, talking about where a graph is increasing in terms of x and not y is one of the hardest concepts in math. Ask me how I know.
Day 2:
Onto the back (which I had planned to have finished yesterday! Ha!)
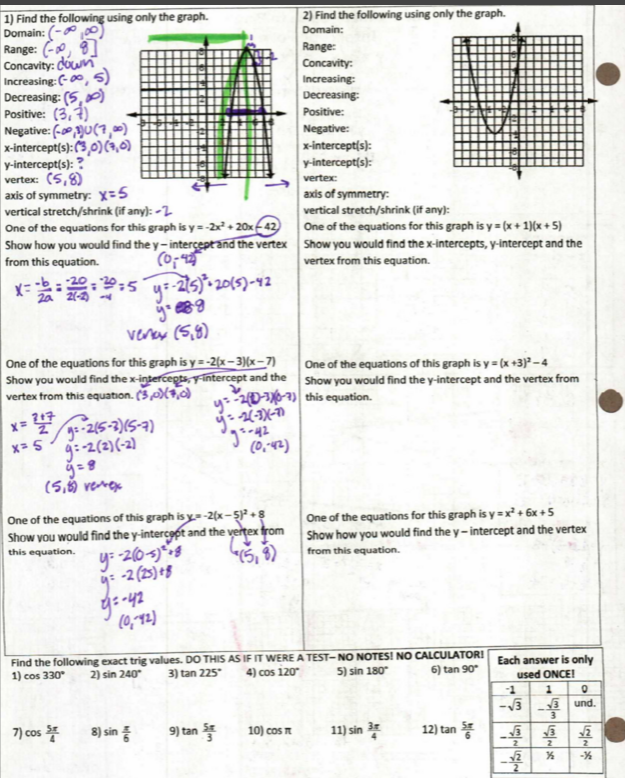
They were in partners and I let them work on each section for 3-5 minutes, then we talked about it. They were doing not horrible, but some didn’t know where to start. Again, in retrospect, I should have put “how to find the vertex” on the front, not “axis of symmetry” because they would tell me there were no instructions for the vertex. (I mean, yeah, except for the box at the bottom of the graph that had “vertex” and an example of each equation, but c’mon, that was all the way at the bottom.) We had about 7 minutes left at the end of class, just enough time for them to cut out their dominoes for tomorrow. The right side was homework. (The bottom was homework the previous night, because they didn’t do so hot on their unit circle test, either. So far this semester has not been off to a great start.)
Day 3: Check homework; at least a quarter of them just wrote down the points under each equation instead of actually showing how we got them (like, you know, the example right next to it). Went through the homework problem and had them work with the Math Shell quadratic dominoes. Based on my previous experience, I had them cut out the graphs and match them to the equations (playing them as dominoes led to lots of silly looking-at-the-wrong-graph mistakes last year when we went to fill in the blanks). Then we rotated partners and checked. Then I revealed the correct answers and maybe 1/4 – 1/3 got them all correct, or had only one pair switched. Then I had them work on filling in the blanks. This seemed to go OK. At the end of the day, I gave them a worksheet that had three equations, asking them to find the important information and graph. In my extra long period, they had time to start on it and there was so much struggle. Like not even knowing where to begin. Like not even knowing that this was the same thing we had been doing for the last three days. Like this was the third day I just wanted to cry at the end of the period.
Day 4: “Ok, I think we maybe need to see the big picture of all these equations again.” So on the back of our worksheet, we did an example together of each of the three types. Then I set them loose on the front again. It was horrible. We have no idea what these numbers are. The x-intercepts are (-1, 0) and (4, 0)? That must mean the vertex is at (-1, 4)! Oh, the vertex is x = 5 and y = 3? Oh, that must mean the x-intercept is 5 and y-intercept is 3. Or the vertex is just x = 5. I went around putting out fires and got most of them through it, but I doubt they would be able to do it again on their own (ok, maybe 15% could).
So this bring us to where we are today: Not much farther in our knowledge of parabolas than we were on Tuesday, perhaps even less (or at least more confused). Also, may I remind you that this is Algebra II, so we’ve already seen these in Algebra I, and I have many, many, many more topics to cover this semester. These extra forms aren’t even in the course of study; I just thought it would be a nice review of parabolas by themselves (we’ve already had a whole chapter on transforming famous parent functions) and practice in seeing the same thing different ways and being able to see why some forms may be better than others.
My question is: do I throw in the towel?
I honestly think it would take at least two more days of practice for them to even be able to attempt a quiz on this. And what could I do differently during those two days that would help them improve? Other than, here is yet another example step-by-step. And I still want to cover completing the square and maybe some applications (as in, where is the ball at its maximum, how long in flight, etc…stuff they’ll see on tests and in other courses). Should I just say, this just wasn’t a good week of lessons. Let’s work on changing standard to vertex because we like vertex form and that’s the only type of graphing that will be on the quiz. Should I try the applications on Monday, which would give them more practice about finding y-intercepts, vertices, and x-intercepts? Should I just forget that last week happened entirely and start the polynomials chapter?
Any advice would be greatly appreciated. Leave it in the comments, or better yet, tweet me (@mathymeg07) so I can pick your brain even more.
Sara Vaughn
January 23, 2016 at 11:03 am
But I did read and thank you!!! If I got nothing else (which is not true), I got this: (barely containing my frustration at both the students for not knowing and myself for being such a crap teacher that I haven’t even gotten this point across in the first semester of Alg II). I am not ALONE!!!! I’m in the same boat–different river–with of all things linear-equations. While commenting on someone’s post this morning, it hit me. This is so flipping boring. Sooo, I’m going to go in with a new approach. Let’s have fun. Let’s create the need for linear equations by collecting data and graphing. Then we can find the critical points meat, information, jazz. I know this is regression/statistics, but I don’t care. I need a spark and/or change or I may be changing out of black into orange. Soooo, with your situation, how bout a problem/situation/story that creates a need for all forms. Maybe like the three little pigs. I know you wanted this tweeted, but like you said. tldr.
Meg Craig
January 23, 2016 at 12:13 pm
No, you’re not in trouble for not tweeting! Some things require more than 140 characters. But I think based on one of the conversations from twitter, I’m going to go the same route as you–let’s put this into a concrete example and see *WHY* these points matter and how we could find them. I’m glad I’m not the only one who has frustration at both students and self…it’s hard to figure out the line between “they should know this” and “I should have taught this better.” Let’s hope both our weeks go better next week…I hope you blog the results! (Hint: I heard the stacking cups activity is super good at this; you may also want to look at Mathalicious’s Domino Effect as a basis for a good talk about y-intercepts and slope(I think it’s still free))
Meg Craig
January 23, 2016 at 12:31 pm
Also, HA on black into orange. 🙂 And thanks for the 140+ character reply!
Eric
January 23, 2016 at 11:35 am
There is a TLDR (Too Long Didn’t Read) at the bottom which summarizes my thoughts.
I feel your agony. When I read through your post it called to mind a question I often ask myself: What is the smallest amount of information they need to know to preform a task? Yes it is true that there are 3 generic forms of a parabola, but do I need to know all 3 to graph it? Do I need to know all 3 to find the zeros? Sure, recognizing that there are more forms helps us answer questions faster, but the barrier to that working is that I must remember more information. I realize the point of the unit was to compare and contrast the different forms so everything I say after this may be of no use to you.
If you do decide to spend more days covering the material, I would recommend refocusing on accomplishing the task versus understanding the specific implications of all of the forms. If a student wants to convert everything into standard form to graph, great. If a student doesn’t know how to factor, okay, use the quadratic formula. Don’t understand how to find the vertex from the equation? Well here’s some graph paper find it that way if you can’t complete the square. I have a general bias against learning something multiple ways. If it takes students 6 to 10 minutes to do something a longer way, ehhh. I am more in favor of teaching students how to adapt and turn something new into something that looks old and familiar.
My theory of learning and knowledge acquisition is to think of what I am teaching as a graph of nodes and edges, in the pure graph theory sense. My first task is to set up a spanning tree instead of creating a complete graph in my students mind. When students have that spanning tree, now its time to add in some extra edges. When I looked at the highly organized ultimate guide to parabolas, I see a complete graph which I believe and you believe was very overwhelming for the majority of students. Possibly leading with how the other two forms are connected to standard form in the future might be a better organizational tool. It gives students the option to either work in new methods or revert back to old methods.
I thought the honesty in your post was very refreshing and I wish you were one of my colleagues. I think that I have grown through reading it and putting myself in your shoes. Thank you for posting. Please feel free to push back on anything that I said. I tried to give you some of my background assumptions on how I approach teaching math in an effort to extend the conversation, not to assert my particular perspective. I think reading the TLDR is a good summary of my thoughts.
TLDR: I might refocus the goal on the tasks of graphing, finding zeros, and finding the vertex of parabolas. De-emphasize which method is “better” for doing one, and how ever the student chooses to do it is fine. This was not the goal of the unit you laid out which was in fact to compare and contrast these forms, but that is how I would approach the situation if I were in your shoes. A retreat instead of throwing in the towel if you will. Help the students find a form they like the best and demonstrate how to adapt to it. Thank you for sharing!
Meg Craig
January 23, 2016 at 12:24 pm
Ok, wow. First of all, thanks for taking the time to write a comment that requires its own TLDR summary. 🙂
Second of all, this is a splendid way to look at this problem and now I can’t believe I’ve never thought of it in this way before. All through precal and calculus we talk about turning what we don’t know into something we do know…this would be perfect as an introduction for that! I was so caught up in my Robot Math Brain (“Input: Vertex Form Output: This is how you find x-int, y-int, and vertex”) that I never stood back and looked at the big picture. In fact, one of my students had her mom help and the mom turned intercept form into standard form and I was like, “well, that was clever!”
And yes, I did want to compare and contrast the three forms, but I think I could still get that by talking about *why* we might want to convert (some think it’s “easier” to find ___ in ____ form, why?) I also wanted them to see it is three ways of talking about the same thing, which I don’t think they got (but they might by being able to convert). (another student example: one matching card gave them the intercept form and asked for b and c of standard form; I got it from graph, but student just said “FOIL the intercept form!” DUH!)
Oh man, now I’m super excited about how to attack this next year. Now need to figure out if it’s fixable this year! Thanks for sharing your thoughts!
Jessy
January 23, 2016 at 12:04 pm
Ugh, I don’t have great advice here, but I feel your struggle. I spend an entire quarter on quadratics (Q3, starting this week!) with my ALG2 classes and don’t even do completing the square (we cover it briefly in PREC). I know my curriculum is technically not within the parameters of a proper ALG2 class, but the truth is that most of the kids just aren’t ready for it. Even with linear functions, most of them struggle to distinguish between the y-intercept & x-intercept and how to find them. Your conversation on day 1 is something I’ve experienced a lot. What sucks is that, conceptually, they can do it… But making the leap from the underlying ideas to a mathematical process is really where their weaknesses are. Which, I’ll take, rather than the other way around (where they can, let’s say, find intercepts all day but have NO IDEA what they mean). The struggle is real. I do have a one-page sheet where instead of giving them the 3 different forms, I list out the 3 different things we care about (y-int, vertex, x-int) with notes on how to find those things and the kids should see that the 3 forms (standard, vertex, factored) nicely align. Anyway, that’s an idea, to kind of have them back into the different forms by asking them about the features first.
Meg Craig
January 23, 2016 at 12:30 pm
Oh, man, now even more to think about! I like the idea of seeing it from the graph and then how each form is helpful. I was trying to do that a bit on the first NTM, but I think I gave away the ending too early! Maybe “this is the x-intercept, do you see this value in any of the three equations?” “Why would that be the case?”
Sadly, I think I have the reverse problem…after four days, they now know to plug in zero to find the y-intercept, but then maybe it will be on the y-axis, or maybe it’s on the y-axis and it’s the vertex, or maybe it’s just some random number we found.
I’m glad I’m not the only one who feels that Alg II is too much for some of the students in Alg II. There is SO MUCH crammed into it and SO MUCH forgotten from Alg I (or even last week!).
Thanks for your thoughtful reply!
Jessy
January 23, 2016 at 1:02 pm
Do you have any idea why our math system goes the way it does? They take a year of ALG1, then a full year “off” during GEOM, then back to ALG2 and they’ve forgotten so much.
Here’s an analogy: I commute by bicycle to work. When I first started doing that, I’d put the bike aside in Dec/Jan and just ride the bus instead (because it’s dark, wet, cold, slippery, whatever). After a two-month break, I’d start riding again in Feb. I’d ride to work & home, and the next day I would be literally TOO SORE to ride. That’s after a relatively short break. How much is lost after several months, or a full year? The brain isn’t much different…
I’m fortunate to work in an independent school, so I can teach the curriculum I want, essentially at the pace I want. My plan for them is, if it’s not helpful for CALC, I throw it out. I’m definitely prioritizing depth over breadth, but sometimes I look at how much stuff we get through, or how far behind where we “should” be, and I just feel awful. But I also work with kids who have missed tons of time in school, have giant knowledge gaps, etc. Even though I understand it, I still can’t help but feel disappointed at how low their skills are by the time they get to me. You just gotta assess where they’re at and make the decision that feels best, I guess.
Laurie Hailer
January 23, 2016 at 2:14 pm
Great analogy. This year I’m teaching Geometry and algebra 2. Knowing about the gap year issues, I’m starting to go over fraction operations and all things algebra 1 with tlmy geomoetry students. I think the new core sequencing will help with this issue, but not quite resolv ed it.
Meg Craig
January 24, 2016 at 7:52 am
Yes! The Alg II teacher thanks you! I think fractions should be (re)taught in every course!
Meg Craig
January 24, 2016 at 7:49 am
I don’t understand the system, either. We used to do a pretty good job at our school of keeping Alg I concepts going in Geometry (usually through warmups), but with some new restructuring of the course and students, it’s gotten more difficult. I’m to the point where I want to slow down and get some concepts down rather than finish everything, especially since I know they’ll see most everything again in Precal (where a lot of this should be moved to in the first place!)
Thanks for the reply and the great analogy!
Laurie Hailer
January 23, 2016 at 2:20 pm
Great post, thanks for sharing. I think this is common. I am trying to spiral some of these things. I think it’s helping a bit. I have totally been where you are and assume I’ll be there again soon. 🙂 I would maybe throw in the towel, for a week, work in something else they will be successful with, and then go back to it. Try a desmos activity. I highly recommend Marbleslides. I had great success with that. I’d love to hear what you decide. Good luck! And remember, these times that feel like stbacks, really help us better understand students needs as we reflect, consult our colleagues, regroup and restart.
Meg Craig
January 24, 2016 at 7:54 am
Thanks for pep talk! I forgot about Marbleslides since it’s so new, maybe I can get the computer lab this week!
Jane Taylor
January 23, 2016 at 2:37 pm
I think, in general, whenever I assume that I can go through some material quickly because they had it the year before, I always find out that I need to reteach it step-by-step because they don’t remember it. Most students take two times to learn something
Meg Craig
January 24, 2016 at 7:58 am
Yes, I always re-learn this every year! I guess I’m the eternal optimist: “Oh, I’m sure they will have remembered this.“
Jane Taylor
January 23, 2016 at 2:40 pm
Another thought: I once had a student tell me that seemed like I was trying to be too efficient in the way I presented material. It was really a wake up call to me as a teacher. When faced with a limited amount of time, I made my notes very compact and efficient, but that was only helpful for me, not for the students. They need to absorb the concepts one at a time, not all at once. Then, at the end, a nice summary of everything might be in order.
Meg Craig
January 24, 2016 at 8:07 am
Interesting…I always pride myself on my beautiful NTMs with all sorts of information organized, but maybe I need to take a step back and reassess. Last year I did talk about each type separately and it did go somewhat better. I think I’ll also take out positive/negative/increasing/decreasing, or at least save it for a different day!
Lee MacArthur
January 24, 2016 at 1:35 am
Unfortunately with all the technology available, its usually easier just to have them graph things on the devices and learn to interpret the data on the associated table. Do we really need to teach this any more? Yes I do struggle with the when to use tech vs when they really need to learn the underlying math. I know my standards say I have to teach it but I’m not sure it is really fully necessary.
Meg Craig
January 24, 2016 at 8:08 am
Unfortunately, we don’t have much technology available in our school on a regular basis, but I do understand your point!
Parabolas Post Mortem – Insert Clever Math Pun Here
March 31, 2016 at 1:44 pm
[…] spent most of last Sunday afternoon trying to take all the suggestions from my last post and put it together into some sort of lesson and this is what I came up […]
Ben
May 17, 2017 at 3:16 pm
That sounds very frustrating. I spent some time thinking about your approach vs. what I’ve been doing at home. (Major caveat: this is me before-schooling my own child 1-on-1 which is a totally different beast but I think some of this transfers.)
First, we spent about 2+ weeks building up to this point rather than jumping in with a huge summary. The text I use starts with completing the squares, works through the quadratic equation in standard form and then comes back to graphing quadratic equations where the standard form for parabolas is introduced. This then explored a bit before being related back to the standard quadratic through completing the square.
But each step in this process was given a bit of time and we stopped to explore parabolas in geogebra i.e. what happens when we modify h,k? What if I want to tilt the parabola? A huge digression to watch a video showing all parabolas are similar.
OK this basically took forever (We work in 10-15 minute increments before the school bus arrives). But I think if you’re going to devote a week anyway to the topic the main point here is that you might skip the summary sheet entirely and work the whole topic as more of a progression/narrative emphasizing the links from stage to stage. For example: while finding x,y intercepts is interesting in its relation to the roots for a graphing unit it fits even better when talking about how to plot and maybe focus on the graphs and plotting them / manipulating them first will let that more naturally fall out in way that contextualizes it. Same for converting between forms. The ease of plotting standard form or using it to identify a vertex, makes it natural to talk about converting a standard quadratic into it. At the end perhaps a summary sheet or maybe even one the students made themselves could be introduced.
I hope this helps and good luck
Meg Craig
July 12, 2017 at 3:22 pm
Great ideas, Ben! I often have the issue of “they should know this already from Alg I; they just need to review, right?” hahaha. If I were to teach it again I would definitely go back to basics as you suggested and summarize last!